题目内容
设不等式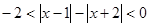 的解集为
的解集为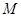 ,
,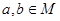 .
.
(Ⅰ)证明: ;
;
(Ⅱ)比较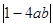 与
与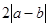 的大小,并说明理由.
的大小,并说明理由.
(Ⅰ)见解析(Ⅱ)|1-4ab|>2|a-b|
解析试题分析:(Ⅰ)利用零点分析法将f(x)=|x-1|-|x+2|化为分段函数,根据分段函数的值域,将不等式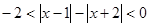 化为不等式-2<-2x-1<0,解得集合M,由
化为不等式-2<-2x-1<0,解得集合M,由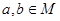 从而得出
从而得出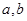 的取值范围,利用含绝对值不等式性质及
的取值范围,利用含绝对值不等式性质及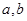 的取值范围,利用放缩法,即可推出所证不等式
的取值范围,利用放缩法,即可推出所证不等式 ;(Ⅱ)先用作出比较法比较|1-4ab|2与4|a-b|2的大小,再利用不等式的开方性质,即可比较出
;(Ⅱ)先用作出比较法比较|1-4ab|2与4|a-b|2的大小,再利用不等式的开方性质,即可比较出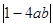 与
与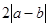 的大小.
的大小.
试题解析:(Ⅰ)记f(x)=|x-1|-|x+2|=
由-2<-2x-1<0解得-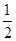 <x<
<x<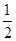 ,则M=(-
,则M=(-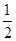 ,
,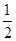 ). 3分
). 3分
所以| a+
a+ b|≤
b|≤ |a|+
|a|+ |b|<
|b|< ×
×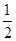 +
+ ×
×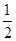 =
=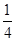 . 6分
. 6分
(Ⅱ)由(Ⅰ)得a2<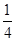 ,b2<
,b2<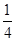 .
.
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0, 9分
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|. 10分
考点:含绝对值不等式解法,含绝对值不等式性质,放缩法,比较法,不等式性质,运算求解能力,转化与化归思想,分类整合思想

练习册系列答案
相关题目
 >
> .
. ,
,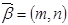 ,其中
,其中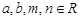 ,由不等式
,由不等式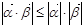 恒成立,可以证明(柯西)不等式
恒成立,可以证明(柯西)不等式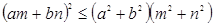 (当且仅当
(当且仅当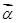 ∥
∥ ,即
,即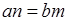 时等号成立),己知
时等号成立),己知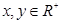 ,若
,若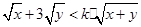 恒成立,利用可西不等式可求得实数
恒成立,利用可西不等式可求得实数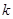 的取值范围是
的取值范围是 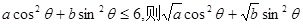 的最大值为 .
的最大值为 .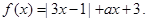
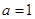 ,解不等式
,解不等式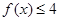 ;
; 有最小值,求
有最小值,求 的取值范围.
的取值范围.
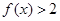 ;
;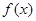 的最小值.
的最小值.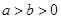 ,且
,且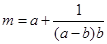 .
.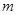 的最小值
的最小值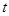 ;
;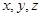 满足
满足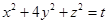 ,求证:
,求证: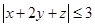 .
.