题目内容
设函数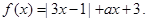
(Ⅰ)若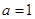 ,解不等式
,解不等式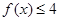 ;
;
(Ⅱ)若函数 有最小值,求
有最小值,求 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:
解题思路:(Ⅰ)讨论 的范围,去掉绝对值符号,再进行求解;(Ⅱ)将解析式化简为分段函数,再根据有最小值求
的范围,去掉绝对值符号,再进行求解;(Ⅱ)将解析式化简为分段函数,再根据有最小值求 的取值范围.
的取值范围.
规律总结:对于含两个绝对值的函数,往往根据 ,讨论
,讨论 的不同范围,将其绝对值符号脱去,转化为分段函数问题.
的不同范围,将其绝对值符号脱去,转化为分段函数问题.
试题解析:(Ⅰ)当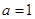 时,
时,
当 时,
时,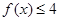 可化为
可化为  ,解得
,解得  ;
;
当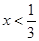 时,
时,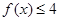 可化为
可化为  ,解得.
,解得.
综上可得,原不等式的解集为
(Ⅱ)
函数 有最小值的充要条件为
有最小值的充要条件为 即
即 .
.
考点:绝对值不等式.

练习册系列答案
相关题目
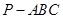 的四个顶点都在半径为4的球面上,且三条侧棱两两互相垂直,则该三棱锥侧面积的最大值为 .
的四个顶点都在半径为4的球面上,且三条侧棱两两互相垂直,则该三棱锥侧面积的最大值为 .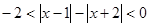 的解集为
的解集为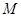 ,
,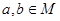 .
. ;
;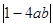 与
与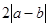 的大小,并说明理由.
的大小,并说明理由.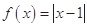 .
.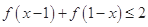 ;
; 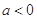 ,求证:
,求证: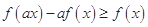
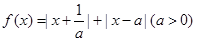
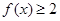 ;
;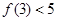 ,求
,求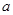 的取值范围.
的取值范围.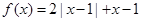 ,
, ,记
,记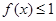 的解集为M,
的解集为M,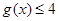 的解集为N.
的解集为N.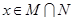 时,证明:
时,证明: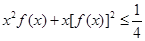 .
.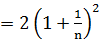 ·an(n∈N+).
·an(n∈N+).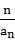 ,求证:c1+c2+c3+…+cn<
,求证:c1+c2+c3+…+cn<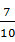 .
. <
< ;②a2>b2;③
;②a2>b2;③ >
>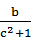 ;④a|c|>b|c|.
;④a|c|>b|c|.