题目内容
已知集合M{x|y=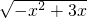
}，N={x||x|＞2}，则M∩N
- A.{x|1＜x＜3}
- B.{x|0＜x＜3}
- C.{x|2＜x＜3}
- D.{x|2＜x≤3
D
分析：先求出集合M的定义域，从而求出集合M，根据绝对值不等式的求解方法求出结合N，最后根据交集的定义求出所求即可．
解答：集合M={x|y=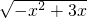}={x|0≤x≤3 }，
集合N={x||x|＞2}={x|x＞2或x＜-2}，
∴M∩N={x|2＜x≤3}，
故选D．
点评：本题考查求偶次根式的定义域的方法，解绝对值不等式的方法，两个集合的交集的定义和求法，属于基础题．
分析：先求出集合M的定义域，从而求出集合M，根据绝对值不等式的求解方法求出结合N，最后根据交集的定义求出所求即可．
解答：集合M={x|y=
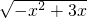}={x|0≤x≤3 }，集合N={x||x|＞2}={x|x＞2或x＜-2}，
∴M∩N={x|2＜x≤3}，
故选D．
点评：本题考查求偶次根式的定义域的方法，解绝对值不等式的方法，两个集合的交集的定义和求法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目