Question

【题目】如图，在平面直角坐标系 中，已知圆 ，点 ，点 ，以B为圆心， 为半径作圆，交圆C于点P，且 的平分线交线段CP于点Q.

（1）当a变化时，点Q始终在某圆锥曲线 上运动，求曲线 的方程；
（2）已知直线l过点C，且与曲线 交于M,N两点，记 面积为 ， 面积为 ，求 的取值范围.

Answer 1

【答案】
（1）解：∵ ,
∴ ,∴ ,
∵ ,∴ ,
由椭圆的定义可知， Q点的轨迹是以C,A为焦点, 2a=4的椭圆，
故点Q的轨迹方程为
（2）解：由题可知，设直线 ，不妨设
∵ ， ，
，
∵ ，∴ ， ，
∴ ，
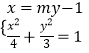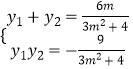∵ ，即 ，
∴ ，
∴ .
【解析】（1）根据题目所给边角关系，可得点Q距两定点A，C的距离和为一定值，符合椭圆的定义，故可得点Q的轨迹方程。
（2）设出直线l的方程，联立椭圆，利用韦达定理求出点的坐标间的关系，求出其变化范围，然后代入面积公式中，即可得到比值。