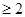题目内容
设 x1、x2(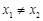 )是函数
)是函数 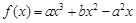 (
(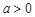 )的两个极值点.
)的两个极值点.
(I)若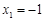 ,
,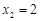 ,求函数
,求函数  的解析式;
的解析式;
(II)若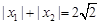 ,求 b 的最大值;
,求 b 的最大值;
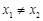 )是函数
)是函数 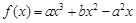 (
(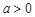 )的两个极值点.
)的两个极值点.(I)若
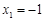 ,
,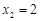 ,求函数
,求函数 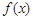 的解析式;
的解析式;(II)若
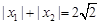 ,求 b 的最大值;
,求 b 的最大值;解:(1) .(经检验,适合)
.(经检验,适合)
(2)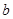 的最大值为
的最大值为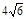 .
.
 .(经检验,适合)
.(经检验,适合)(2)
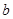 的最大值为
的最大值为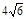 .
.本题考查函数解析式的求法和实数b的最大值的求法,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,仔细解答,注意导数性质的灵活运用
(1)由f(x)=ax3+bx2-a2x(a>0),知f'(x)=3ax2+2bx-a2(a>0)依题意有 f′(-1)=0,
f′(2)=0,
由此能求出f(x).(2)由f'(x)=3ax2+2bx-a2(a>0),知x1,x2是方程f'(x)=0的两个根,且|x1|+|x2|=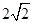 ,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值
,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值
(1)由f(x)=ax3+bx2-a2x(a>0),知f'(x)=3ax2+2bx-a2(a>0)依题意有 f′(-1)=0,
f′(2)=0,
由此能求出f(x).(2)由f'(x)=3ax2+2bx-a2(a>0),知x1,x2是方程f'(x)=0的两个根,且|x1|+|x2|=
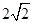 ,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值
,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
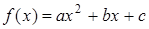 中
中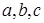 均为实数,且满足
均为实数,且满足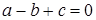 ,对于任意实数
,对于任意实数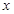 都有
都有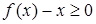 ,并且当
,并且当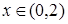 时有
时有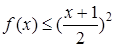 成立。
成立。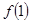 的值;
的值; 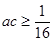 ;
; 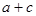 取最小值时,函数
取最小值时,函数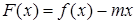 (
(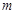 为实数)是单调函数,求证:
为实数)是单调函数,求证: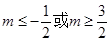 。
。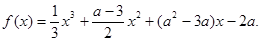
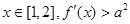 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;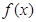 的两个极值点分别为
的两个极值点分别为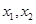 判断下列三个代数式:
判断下列三个代数式: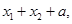 ②
②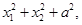 ③
③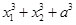 中有几个为定值?并且是定值请求出;
中有几个为定值?并且是定值请求出;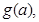 并求出
并求出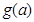 的最小值.
的最小值.  与
与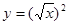
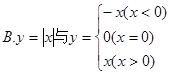
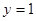 与
与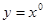
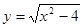 (x∈Z)与
(x∈Z)与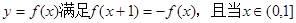 时单调递增,
时单调递增,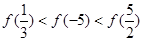
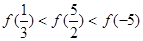
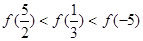
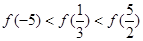
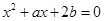 的两根为
的两根为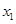 、
、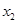 ,且
,且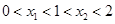 则
则 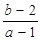 的取值范围是( )
的取值范围是( )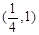
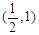
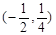

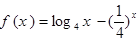 ,
,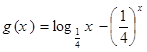 的零点分别为
的零点分别为 ,则( )
,则( )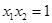
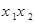 <1
<1