题目内容
已知数列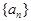 是等差数列,且
是等差数列,且 ,
, ,
,
(1)求数列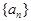 的通项公式; (2)令
的通项公式; (2)令 ,求数列
,求数列 前n项和
前n项和 .
.
(1)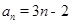 (2)
(2)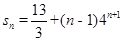
解析试题分析:解:(1)数列{an}是等差数列,且a1=1,a1+a2+a3=12,设出公差为d,∴a1+a1+d+a1+2d=12,∴a1+d=4,可得2+d=4,解得d=2,∴an=a1+(n-1)d=1+(n-1)×2=2n+1,(2)数列{an}的通项公式为an=n•2n,设其前n项和为Sn,∴Sn=1•21+2•22+3•23+…+n•2n①
2Sn=1•22+2•23+3•24+…+n•2n+1②
①-②可得-Sn=21+22+23+…+2n-n•2n+1②
∴-Sn=-2+22+23++…+2n -n•2n+1,
∴Sn=n×2n+1-2n+1+2=(n-1)2n+1+2;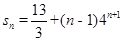
考点:等差数列,数列的求和
点评:主要是考查了等差数列的定义,以及通项公式的运用,以及错位相减法来求解数列的和,属于中档题。

练习册系列答案
相关题目
 满足
满足 ,
,
 ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前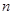 项和为
项和为
 ,对于任意的
,对于任意的 恒有
恒有

 的通项公式
的通项公式
 证明:
证明:
 的等比数列
的等比数列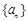 的前n项和为
的前n项和为 , 且
, 且 成等差数列.
成等差数列.  .
.  中,已知
中,已知 .
. 是等差数列;
是等差数列; 满足
满足 ,求
,求 .
. ,
, ,
, ,记
,记
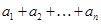 ,
,
 ,
,
 (
( ),若对于任意
),若对于任意 ,
, ,
, 成等差数列.
成等差数列. 的前
的前 项和.
项和. 的首项
的首项 ,且
,且 (
( )
) ,求证:数列
,求证:数列 为等差数列;②设
为等差数列;②设 ,求数列
,求数列 的前
的前 项和
项和 。
。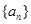 前n项和
前n项和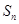 ,且
,且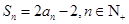 .
. ,求数列
,求数列 的前
的前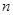 项和
项和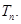
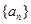 中,
中,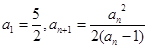
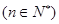 ,用数学归纳法证明:
,用数学归纳法证明: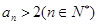 。
。