题目内容
已知数列 的首项
的首项 ,且
,且 (
( )
)
①设 ,求证:数列
,求证:数列 为等差数列;②设
为等差数列;②设 ,求数列
,求数列 的前
的前 项和
项和 。
。
① 得
得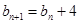 ,
, ;
;
②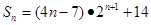 。
。
解析试题分析:①证明:∵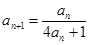
∴
又 ∴
∴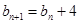

∴数列 为等差数列。 (4分)
为等差数列。 (4分)
②解:∵数列 的首项为
的首项为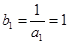 ,公差
,公差 的等差数列
的等差数列
∴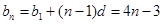 (6分)
(6分)
∴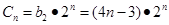
∴
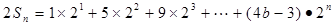
∴

∴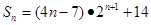 (12分)
(12分)
考点:等差数列、等比数列的概念通项公式,错位相减法。
点评:中档题,确定数列的通项公式,往往利用已知条件,建立相关元素的方程组,以达到解题目的。定义法常常是证明数列是等差数列、等比数列的常用方法。“分组求和法”“裂项相消法”“错位相减法”等,是高考常常考查的数列求和方法。

练习册系列答案
相关题目
 }中,
}中, ,又
,又 成等比数列.
成等比数列. ,求数列{
,求数列{ }的前n项和
}的前n项和 .
.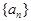 是等差数列,且
是等差数列,且 ,
, ,
, ,求数列
,求数列 前n项和
前n项和 .
.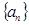 中,
中, ,n≥2时
,n≥2时 ,求通项公式.
,求通项公式.  是数列
是数列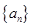 的前
的前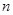 项和,且对任意
项和,且对任意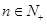 ,有
,有 ,
,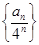 的通项公式;
的通项公式; 的前
的前 .
. ,数列
,数列 满足
满足 。
。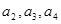 ;
;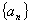 中,
中,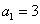 ,满足
,满足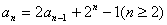 。
。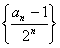 为等差数列;
为等差数列;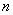 项和
项和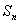 .
. 的前
的前 项和为
项和为 ,且方程
,且方程 有一个根为
有一个根为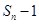 ,
, .
.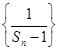 是等差数列;
是等差数列;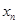 ,数列
,数列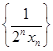 的前
的前 ,求
,求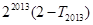 的值;
的值;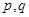 ,使得
,使得 ,
, ,
, 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的 中,
中,
 ,求数列
,求数列 的前n项和
的前n项和 .
.