题目内容
【题目】如图(1)所示,在直角梯形ABCD中, ![]() ,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示. 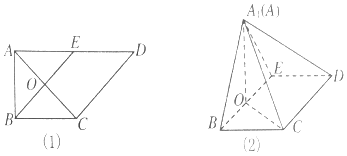
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
【答案】
(1)证明:在图(1)中,因为 ![]() ,E是AD的中点,且
,E是AD的中点,且 ![]() ,
,
所以BE⊥AC,BE∥CD,
即在图(2)中,BE⊥OA1,BE⊥OC,又OA1∩OC=O,OA1平面A1OC,OC平面A1OC,
从而BE⊥平面A1OC,又BE∥CD,所以CD⊥平面A1OC
(2)解:由已知,平面A1BE⊥平面BCDE,且交线为BE,
又由(1)知,BE⊥OA1,所以OA1⊥平面BCDE,
如图,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
设 ![]() ,所以
,所以 ![]() ,
,
得 ![]() .
.
设平面A1BC的法向量 ![]() ,平面A1CD的法向量
,平面A1CD的法向量 ![]() ,
,
平面A1BC与平面A1CD的夹角为θ,
则 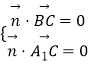 得
得 ![]() ,取
,取 ![]() ,同理,取
,同理,取 ![]() ,
,
从而 ![]() ,
,
即平面A1BC与平面A1CD所成锐二面角的余弦值为 ![]() .
.
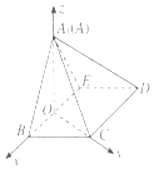
【解析】(1)BE⊥平面A1OC,又BE∥CD,即可证明:CD⊥平面A1OC;(2)若平面A1BE⊥平面BCDE,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,求出平面的法向量,即可求平面A1BC与平面A1CD所成锐二面角的余弦值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目