Question

【题目】在四棱锥P﹣ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA=AB，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则剩余部分体积与原四棱锥体积的比值为（ ）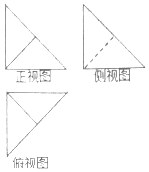

A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：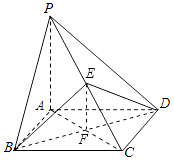

根据几何体的三视图可得；
该几何体是过BD且平行于PA的平面截四棱锥P﹣ABCD所得的几何体．
设AB=1，则截取的部分为三棱锥E﹣BCD，
V三棱锥E﹣BCD= × ×1×1× = ．
V四棱锥P﹣ABCD= = = ．
剩余部分的体积V剩余部分=V四棱锥P﹣ABCD﹣V三棱锥E﹣BCD= ﹣ = ．
∴剩余部分体积与原四棱锥体积的比值= = ．
故选：D．
【考点精析】认真审题，首先需要了解由三视图求面积、体积(求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积)．