题目内容
(本题10分)已知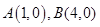 ,动点
,动点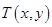 满足
满足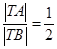 ,设动点
,设动点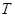 的轨迹是曲线
的轨迹是曲线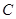 ,直线
,直线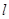 :
: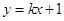 与曲线
与曲线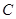 交于
交于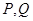 两点.(1)求曲线
两点.(1)求曲线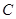 的方程;
的方程;
(2)若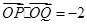 ,求实数
,求实数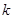 的值;
的值;
(3)过点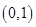 作直线
作直线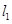 与
与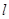 垂直,且直线
垂直,且直线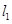 与曲线
与曲线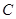 交于
交于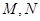 两点,求四边形
两点,求四边形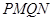 面积的最大值.
面积的最大值.
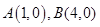 ,动点
,动点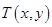 满足
满足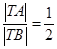 ,设动点
,设动点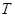 的轨迹是曲线
的轨迹是曲线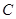 ,直线
,直线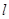 :
: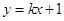 与曲线
与曲线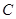 交于
交于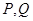 两点.(1)求曲线
两点.(1)求曲线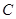 的方程;
的方程;(2)若
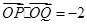 ,求实数
,求实数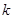 的值;
的值;(3)过点
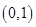 作直线
作直线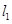 与
与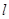 垂直,且直线
垂直,且直线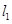 与曲线
与曲线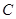 交于
交于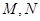 两点,求四边形
两点,求四边形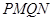 面积的最大值.
面积的最大值.(1)曲线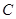 的方程为
的方程为 ;(2)
;(2) 。
。
(3)当 时,四边形
时,四边形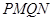 面积有最大值7.
面积有最大值7.
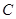 的方程为
的方程为 ;(2)
;(2) 。
。(3)当
 时,四边形
时,四边形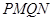 面积有最大值7.
面积有最大值7.试题分析:(1)设
 为曲线
为曲线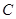 上任一点,则由
上任一点,则由 ,化简整理得
,化简整理得 。
。 (2)因为根据向量的关系式,
 ,所以
,所以 ,
, 所以圆心到直线
所以圆心到直线 的距离
的距离 ,所以
,所以
(3)对参数k,分情况讨论,当
 时,
时, ,
,
当
 时,圆心到直线
时,圆心到直线 的距离
的距离 ,所以
,所以
 ,同理得|PQ|,求解四边形的面积。
,同理得|PQ|,求解四边形的面积。解:(1)设
 为曲线
为曲线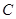 上任一点,则由
上任一点,则由 ,化简整理得
,化简整理得 。
。 曲线
曲线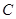 的方程为
的方程为 --------------3分
--------------3分 (2)因为
 ,所以
,所以 ,
,
所以圆心到直线
 的距离
的距离 ,所以
,所以 。 -----6分
。 -----6分(3)当
 时,
时, ,
,
当
 时,圆心到直线
时,圆心到直线 的距离
的距离 ,所以
,所以
 ,同理得
,同理得
所以

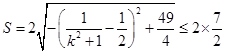 =7当且仅当
=7当且仅当 时取等号。
时取等号。所以当
 时,
时,
综上,当
 时,四边形
时,四边形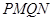 面积有最大值7. --11
面积有最大值7. --11点评:解决该试题的关键是设出所求点满足的关系式,化简得到轨迹方程,同时利用联立方程组的思想得到长度和面积的表示。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
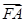 +
+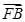 +
+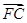 =0,则|
=0,则| 轴的距离少1.
轴的距离少1. 于
于 点,且
点,且 ,
, ,
, 的值。
的值。 有相同的焦点,直线y=
有相同的焦点,直线y=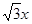 为
为 的一条渐近线.
的一条渐近线.  (0,4)的直线
(0,4)的直线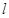 ,交双曲线
,交双曲线 点(
点( =
=
 ,且
,且 时,求
时,求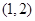 总可作两条直线与圆
总可作两条直线与圆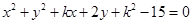 相切,则实数
相切,则实数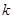 的取值范围是 .
的取值范围是 . 的焦点为
的焦点为 ,准线为
,准线为 ,过
,过 ;
; 的值.
的值.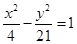 ,
,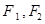 分别为它的左、右焦点,
分别为它的左、右焦点,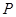 为双曲线上一点,
为双曲线上一点,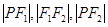 成等差数列,则
成等差数列,则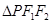 的面积为 .
的面积为 . 、
、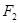 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则



 的离心率为2,有一个焦点恰好是抛物线
的离心率为2,有一个焦点恰好是抛物线 的焦点,则此双曲线的渐近线方程是 ( )
的焦点,则此双曲线的渐近线方程是 ( )


