题目内容
【题目】(1)已知椭圆两个焦点的坐标分别是(-2,0)，(2,0)，并且经过点
，求它的标准方程；
（2）已知双曲线两个焦点的坐标分别是(0,-6)，(0,6)，并且经过点(2,-5)，求它的标准方程.
【答案】(1) 
(2) 
【解析】
（1）由题意可设椭圆方程为
，且
，利用椭圆定义及两点间的距离公式求得
，结合隐含条件求得
，则椭圆方程可求；
（2）由题意可设双曲线的方程为
，且
，利用双曲线的定义及两点间的距离公式求得，结合隐含条件求得，则双曲线方程可求.
因为椭圆的焦点在
轴上，所以设它的标准方程为
有椭圆的定义知
，
又因为，所以
因此，所求椭圆的标准方程为
.
（2）因为双曲线的焦点在
轴上，所以设它的标准方程为
有双曲线的定义知
，
又因为，所以
因此，所求双曲线的标准方程为.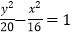
【题目】某地区高考实行新方案，规定：语文、数学和英语是考生的必考科目，考生还须从物理，化学，生物，历史，地理和政治六个科目中选取三个科目作为选考科目．若一个学生从六个科目中选出了三个科目作为选考科目，则称该学生的选考方案确定；否则，称该学生选考方案待确定．例如，学生甲选择“物理、化学和生物”三个选考科目，则学生甲的选考方案确定，“物理、化学和生物”为其选考方案．
某学校为了解高一年级420名学生选考科目的意向，随机选取30名学生进行了一次调查，统计选考科目人数如下表：
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
（Ⅰ）估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
（Ⅱ）假设男生、女生选择选考科目是相互独立的．从选考方案确定的8位男生中随机选出1人，从选考方案确定的10位女生中随机选出1人，试求该男生和该女生的选考方案中都含有历史学科的概率；
（Ⅲ）从选考方案确定的8名男生中随机选出2名，设随机变量
，求
．
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数 |
|
|
|
|
加工的时间 |
|
|
|
|
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出
关于
的线性回归方程
.
（3）试预测加工
个零件需要多少时间？
附录：参考公式：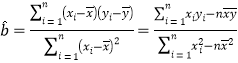
，
.
