题目内容
函数f(x)=x2-2x+3,若|f(x)-a|<2恒成立的充分条件是1≤x≤2,则实数a的取值范围是______.
∵|f(x)-a|<2恒成立的充分条件是1≤x≤2,
∴当1≤x≤2时,|f(x)-a|<2恒成立,
即-2<f(x)-a<2,
∴a-2<f(x)<2+a恒成立,
∵1≤x≤2,
∴2≤f(x)≤3,
∴要使a-2<f(x)<2+a恒成立,
则
,
即
,
∴1<a<4,
故答案为:1<a<4
∴当1≤x≤2时,|f(x)-a|<2恒成立,
即-2<f(x)-a<2,
∴a-2<f(x)<2+a恒成立,
∵1≤x≤2,
∴2≤f(x)≤3,
∴要使a-2<f(x)<2+a恒成立,
则
|
即
|
∴1<a<4,
故答案为:1<a<4

练习册系列答案
相关题目
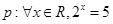 ,则
,则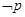 为( )
为( )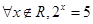
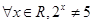
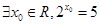
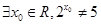
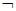 q)”是假命题;③命题“(
q)”是假命题;③命题“( ”的否定是( )
”的否定是( )


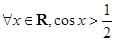
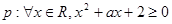 ,则
,则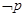 是_____________________________
是_____________________________