题目内容
3. 如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.
如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.
分析 可取B1C1中点E,并且连接A1E,CE,ED,则容易说明四边形B1ECD为平行四边形,从而得到EC∥B1D,这样便根据线面平行的判定定理得出EC∥平面AB1D,而同理可说明A1E∥平面AB1D,这样便可得出平面A1EC∥平面AB1D,从而得出A1C∥平面AB1D.
解答  证明:如图,取B1C1中点E,连接A1E,CE,ED;
证明:如图,取B1C1中点E,连接A1E,CE,ED;
D为BC的中点,E为B1C1中点;
∴B1E=DC,且B1E∥BC;
∴四边形B1ECD为平行四边形;
∴EC∥B1D,B1D?平面AB1D,EC?平面AB1D;
∴EC∥平面AB1D;
同理,四边形EDAA1为平行四边形;
∴A1E∥AD;
∴A1E∥平面AB1D;
又A1E∩EC=E;
∴平面A1EC∥平面AB1D;
又A1C?平面A1EC;
∴A1C∥平面AB1D.
点评 考查平行四边形的定义,三棱柱的侧面为平行四边形,线面平行的判定定理,以及面面平行的判定定理,面面平行的性质.

练习册系列答案
相关题目
13.点F(c,0)为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,点P为双曲线左支上一点,线段PF与圆x2+y2=$\frac{{b}^{2}}{4}$相切于点Q,且$\overrightarrow{PQ}$=$\frac{1}{2}$$\overrightarrow{PF}$,则双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
15.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1与直线y=x+b相切,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
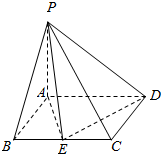 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.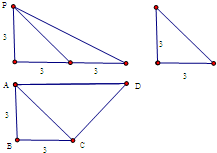 已知四棱锥P-ABCD的三视图如图所示,
已知四棱锥P-ABCD的三视图如图所示, 已知:正方体ABCD-A1B1C1D1,边长为1,E为棱CC1的中点.
已知:正方体ABCD-A1B1C1D1,边长为1,E为棱CC1的中点.