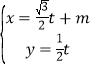题目内容
【题目】已知椭圆
（
为参数），A，B是C上的动点，且满足
（O为坐标原点），以原点O为极点，x轴的正半轴为极轴建立坐标系，点D的极坐标为
.
（1）求椭圆C的极坐标方程和点D的直角坐标；
（2）利用椭圆C的极坐标方程证明
为定值.
【答案】（1）
，
；（2）证明见解析
【解析】
（1）利用参数方程、极坐标方程与直角坐标方程的互化公式即可求出椭圆C的极坐标方程，再利用极坐标与直角坐标的互化公式求出点D的直角坐标即可；
（2）利用（1）中椭圆C的极坐标方程，设
，
，根据极坐标系中
和
的定义，结合三角函数诱导公式即可证明.
（1）由题意可知，椭圆C的普通方程为
，
把
代入椭圆C的普通方程可得，
椭圆C的极坐标方程为，
因为点D的极坐标为
，
所以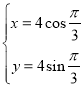
，解得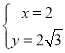
，
所以点D的直角坐标为.
（2）证明：由（1）知，椭圆C的极坐标方程为，
变形得
，
由
，不妨设，，
所以
，
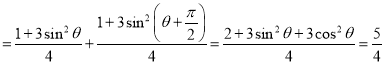所以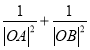
为定值
.
【题目】在信息时代的今天，随着手机的发展，“微信”越来越成为人们交流的一种方式，某机构对“使用微信交流”的态度进行调查，随机抽取了100人，他们年龄的频数分布及对“使用微信交流”赞成的人数如下表：（注：年龄单位：岁）
年龄 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
（1）若以“年龄45岁为分界点”，由以上统计数据完成下面的2×2列联表，并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”？
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
若从年龄在[55，65），[65，75）的别调查的人中各随机选取两人进行追踪调查，记选中的4人中赞成“使用微信交流”的人数为X，求随机变量X的分布列及数学期望．
参考数据：
P（K2≥k0） | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式：K2=
，其中n=a+b+c+d．
