题目内容
【题目】椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,右顶点为B,且满足
,右顶点为B,且满足![]()
![]() Ⅰ
Ⅰ![]() 求椭圆的离心率e;
求椭圆的离心率e;
![]() Ⅱ
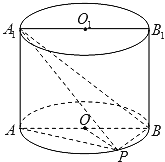
Ⅱ![]() 设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点
设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点![]() ,问是否存在过
,问是否存在过![]() 的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)存在满足条件的直线,斜率为
;(Ⅱ)存在满足条件的直线,斜率为![]() .
.
【解析】
![]() 根据
根据![]() 可得
可得![]() ,即可求出椭圆的离心率,
,即可求出椭圆的离心率,
![]() 由已知得
由已知得![]() ,
,![]() 故椭圆方程为
故椭圆方程为![]() ,设
,设![]() ,求出点P的坐标,再求出线段PB为直径的圆的圆心坐标,根据直线和圆的位置关系可得.
,求出点P的坐标,再求出线段PB为直径的圆的圆心坐标,根据直线和圆的位置关系可得.
解:![]() ,右顶点为B,
,右顶点为B,
![]() 为等腰三角形,
为等腰三角形,
![]() ,
,
由![]() ,
,
![]() 椭圆的离心率
椭圆的离心率![]() .
.
![]() 由已知得
由已知得![]() ,
,![]() .
.
故椭圆方程为![]() ,设
,设![]() 由
由![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又因为点P在椭圆上,故![]() ,
,
由以上两式可得![]() ,
,
![]() 点P不在椭圆的顶点,
点P不在椭圆的顶点,
![]() ,
,![]() ,
,
故![]() ,
,
设圆的圆心为![]() ,则
,则![]() ,
,![]() ,
,
则圆的半径![]() ,
,
假设存在过![]() 的直线满足题设条件,并设该直线的方程为
的直线满足题设条件,并设该直线的方程为![]() ,
,
由相切可知![]() ,
,
![]()
即得![]() ,解得
,解得![]()
故存在满足条件的直线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
(1)根据表,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
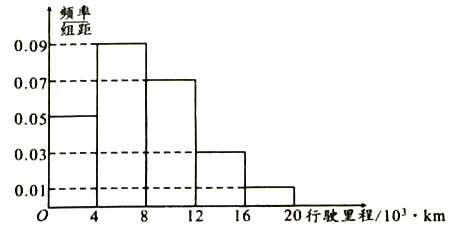
(2)图给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法从![]() 岁以上车主中抽取
岁以上车主中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送免费保养券,求这
人赠送免费保养券,求这![]() 人中至少有
人中至少有![]() 辆轿车的概率。
辆轿车的概率。
附:![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|