题目内容
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)求第2分钟末没有人买晚饭的概率;
(Ⅱ)估计第三个学生恰好等待4分钟开始买饭的概率.
(Ⅰ)第2分钟末没有人买晚饭的概率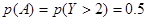 ;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率
;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率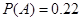 .
.
解析试题分析:(Ⅰ)求第2分钟末没有人买晚饭的概率,对于第2分钟末没有人买到饭这个事件,实际上是第一个学生买饭所需的时间超过2分钟,由统计表易求出;(Ⅱ)估计第三个学生恰好等待4分钟开始买饭的概率,包括①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.这三个事件,根据互斥事件的概率求法,即可求出概率.
试题解析:(Ⅰ)记‘第2分钟末没有人买到饭’为A事件,即是第一个学生买饭所需的时间超过2分钟, 所以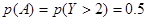 ..(6分)
..(6分)
(Ⅱ) 表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形: ①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.
表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形: ①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.
所以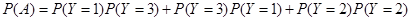
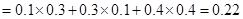 (12分)
(12分)
考点:互斥事件的概率.

练习册系列答案
相关题目
在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
(2)若这2人来自区域A,D,并记来自区域A队员中的人数为X,求随机变量X的分布列及数学期望.
为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为
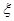 ,求随机变量
,求随机变量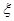 的分布列,及数学期望.
的分布列,及数学期望.  表示.
表示.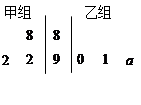
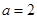 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为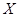 ,求随机变量
,求随机变量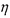 的方差是多少?
的方差是多少?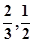 且每棵树是否存活互不影响,求移栽的5棵树中:
且每棵树是否存活互不影响,求移栽的5棵树中: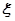 的分布列与期望.
的分布列与期望.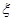 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)

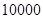 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是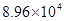 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;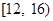 范围内的家庭中选出
范围内的家庭中选出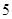 户作为采访对象,其中在
户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求