题目内容
3.设f(x)=x2-2mx+2,当x∈[-1,+∞)时,f(x)≥m恒成立,求实数m的取值范围.分析 将二次函数进行配方,利用二次函数的图象和性质求解,要使不等式f(x)≥m恒成立,则只需求出函数在x∈[-1,+∞]时的最小值即可.
解答 解:∵f(x)=x2-2mx+2,当x∈[-1,+∞)时,f(x)≥m恒成立,
即g(x)=x2-2mx+2-m=(x-m)2+2-m-m2≥0,当x∈[-1,+∞)时,恒成立,
∴函数g(x)的对称轴是x=m,
①m≤-1时,g(x)min=g(-1)=m+3,
∴只需m+3≥0即可,
∴-3≤m≤-1,
②m>-1时,g(x)min=g(m)=2-m-m2,
∴只需2-m-m2≥0即可,
∴-1<m≤1,
综上:-3≤m≤1.
点评 本题主要考查二次函数的图象和性质,要注意分别讨论对称轴和区间之间的关系确定函数的最小值.

练习册系列答案
相关题目
15.设M={y|y=2x,x∈R},N={y|y=x2,x∈R},则( )
| A. | M∩N={(2,4)} | B. | M∩N={(2,4),(4,16)} | C. | M=N | D. | M?N |
12.设A,B是双曲线x2-y2=1上关于原点O对称的两点,将坐标平面沿双曲线的一条渐近线l折成直二面角,则折叠后线段AB长度的最小值为( )
| A. | $\sqrt{2\sqrt{2}}$ | B. | $\sqrt{3\sqrt{2}}$ | C. | $\sqrt{2}$ | D. | 3 |
20.假如今年省运会给岭师附中高中三个年级7个自主推荐的志愿者名额,则每个年级至少分到一个名额的方法数为( )
| A. | 10 | B. | 15 | C. | 21 | D. | 30 |
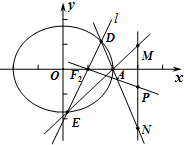 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点$B(0,\sqrt{3})$为短轴的一个端点,∠OF2B=60°.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点$B(0,\sqrt{3})$为短轴的一个端点,∠OF2B=60°.