题目内容
(本小题满分12分)已知数列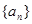 是等差数列,
是等差数列,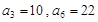 ,数列
,数列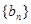 的前n项和是
的前n项和是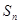 ,且
,且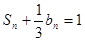 .
.
(I)求数列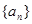 的通项公式;
的通项公式;
(II)求证:数列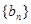 是等比数列;
是等比数列;
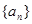 是等差数列,
是等差数列,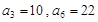 ,数列
,数列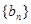 的前n项和是
的前n项和是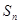 ,且
,且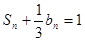 .
.(I)求数列
 的通项公式;
的通项公式;(II)求证:数列
 是等比数列;
是等比数列;(1) 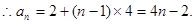
(2)根据等比数列的定义,相邻两项的比值为定值得到证明。
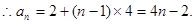
(2)根据等比数列的定义,相邻两项的比值为定值得到证明。
试题分析:解:(1)由已知
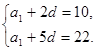 解得
解得 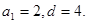 …………4分
…………4分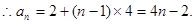 ………………6分
………………6分(2)令
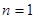 ,得
,得 解得
解得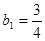 , ………7分
, ………7分由于
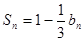 , ①
, ①当
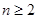 时,
时,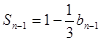 ②
②-②得
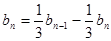 ,
, 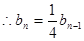 ……………10分
……………10分又
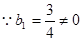 ,
, 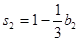 ,
,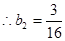 ,满足
,满足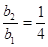
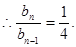
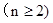
∴数列
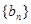 是以
是以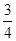 为首项,
为首项,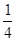 为公比的等比数列. ……………………12分
为公比的等比数列. ……………………12分点评:本试题是基础题,考查了基本概念,基本运算,细心运算,一般不会出错,是一道基础题。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 n}满足
n}满足 .
. M;
M;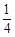 ]时,求证:
]时,求证: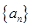 的前
的前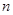 项和为
项和为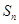 ,且
,且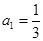 ,
,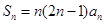
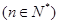 .
.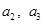 的值;
的值;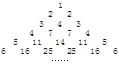
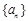 满足:
满足: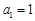 ,
,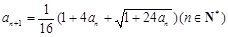 。
。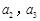 ;
; 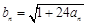 ,求数列
,求数列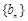 的通项公式;
的通项公式; 中
中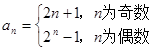 , 则
, 则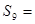 。
。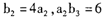
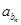 <0.001成立的最小的n值.
<0.001成立的最小的n值.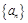 中的各项均为正数,且满足
中的各项均为正数,且满足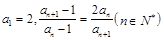 .记
.记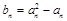 ,数列
,数列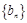 的前
的前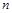 项和为
项和为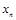 ,且
,且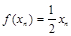 .
. 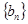 是等比数列;
是等比数列;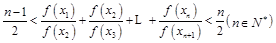 .
.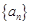 中,
中,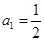 ,
,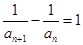 .
. 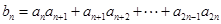 ,求
,求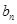 的最大值。
的最大值。