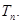题目内容
(本题满分14分)已知数列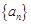 中,
中,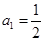 ,
,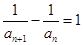 .
.
⑴ 求出数列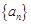 的通项公式;
的通项公式;
⑵ 设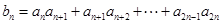 ,求
,求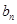 的最大值。
的最大值。
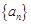 中,
中,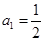 ,
,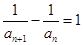 .
. ⑴ 求出数列
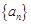 的通项公式;
的通项公式;⑵ 设
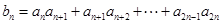 ,求
,求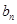 的最大值。
的最大值。(1)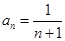 ;(2)
;(2)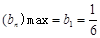 。
。
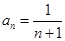 ;(2)
;(2)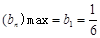 。
。试题分析:(1)本试题主要是利用递推关系式得到
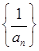 是以2为首项,1为公差的等差数列,进而得到通项公式。(2)利用第一问的结论,结合裂项法求和得到bn,求解其最值。
是以2为首项,1为公差的等差数列,进而得到通项公式。(2)利用第一问的结论,结合裂项法求和得到bn,求解其最值。解:(1)∵
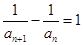
∴
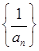 是以2为首项,1为公差的等差数列…2分
是以2为首项,1为公差的等差数列…2分∴
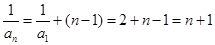 …………5分
…………5分 ∴
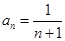 , ∴数列
, ∴数列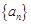 的通项公式为
的通项公式为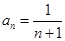 ………6分
………6分(2)
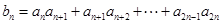
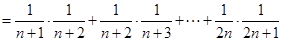
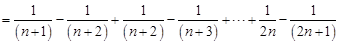
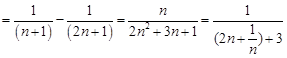 ………10分
………10分令
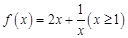 ,则
,则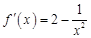 , 当
, 当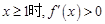 恒成立
恒成立∴
 在
在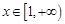 上是增函数,故当
上是增函数,故当 时,
时,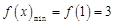 …13分
…13分 即当
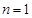 时,
时, 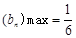 ………14分
………14分 另解:
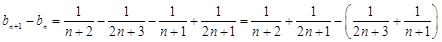
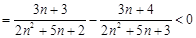
∴ 数列
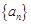 是单调递减数列,∴
是单调递减数列,∴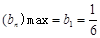
点评:解决该试题的关键是能根据已知的递推关系,结合等差数列的定义得到数列an的通项公式,进而得到anan+1的通项公式,采用裂项法得到和式。

练习册系列答案
相关题目
 是区域
是区域 ,(
,( )内的点,目标函数
)内的点,目标函数 ,
, 的最大值记作
的最大值记作 .若数列
.若数列 的前
的前 项和为
项和为 ,
,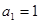 ,且点(
,且点( )在直线
)在直线 上.
上. 为等比数列;
为等比数列; 的前
的前 .
. ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。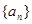 是等差数列,
是等差数列,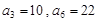 ,数列
,数列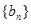 的前n项和是
的前n项和是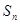 ,且
,且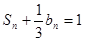 .
.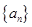 是等差数列,
是等差数列,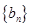 是各项为正数的等比数列,且
是各项为正数的等比数列,且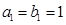 ,
,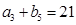 ,
,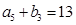 .
. 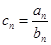 ,求数列
,求数列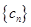 的前
的前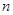 项和
项和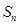 .
.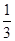 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是 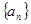 中,
中,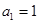 ,且对于任意正整数n,都有
,且对于任意正整数n,都有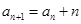 ,则
,则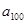 =______
=______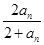 (n∈N*).
(n∈N*).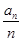 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。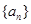 为等比数列,
为等比数列,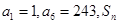 为等差数列
为等差数列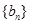 的前n项和,
的前n项和,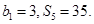
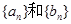 的通项公式;
的通项公式;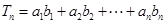 ,求
,求