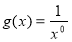题目内容
5.函数f(x)=$\left\{\begin{array}{l}{x+1,0≤x<3}\\{-1,x<0}\end{array}\right.$的定义域为(-∞,3),值域为{-1}∪[1,4).分析 直接利用已知条件求解函数的定义域以及值域即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{x+1,0≤x<3}\\{-1,x<0}\end{array}\right.$的定义域为:(-∞,3);
x∈[0,3),f(x)∈[1,4),
x<0时,f(x)=-1.
函数的值域为:{-1}∪[1,4).
故答案为:(-∞,3);{-1}∪[1,4)
点评 本题考查函数的值域以及函数的定义域的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知函数y=$\frac{{x}^{2}}{2}$的定义域为[-2,2],则y=f(x)的值域为( )
| A. | [-1,1] | B. | [1,2] | C. | [0,2] | D. | [0,3] |
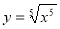 与
与
 与
与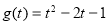 (
(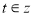 )
) 与
与
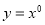 与
与