题目内容
17.已知函数y=$\frac{{x}^{2}}{2}$的定义域为[-2,2],则y=f(x)的值域为( )| A. | [-1,1] | B. | [1,2] | C. | [0,2] | D. | [0,3] |
分析 直接由二次函数的单调性求得函数的值域.
解答 解:∵y=$\frac{{x}^{2}}{2}$的定义域为[-2,2],
∴当x=0时函数y=f(x)有最小值0,
当x=-2(或2)时函数有最大值为2.
∴y=f(x)的值域为[0,2].
故选:C.
点评 本题考查函数的值域及其求法,考查了二次函数的单调性,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若n∈N*,则$\sqrt{{4}^{-n}+{2}^{1-n}+1}$+$\sqrt{{4}^{-n}-{2}^{1-n}+1}$=( )
| A. | 2 | B. | 2-n | C. | 21-n | D. | 2-2n |
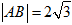 ,则圆C的内接正三角形的面积为( )
,则圆C的内接正三角形的面积为( )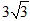 D.
D. 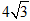
 的集合
的集合 的所有可能情况是
的所有可能情况是