题目内容
10.设{an}是公差为-2的等差数列,且a1+a4+a7+…+a25+a28=90,则a4+a6+a8+…+a48+a50=-384.分析 由等差数列的性质可得a1+a4+a7+…+a25+a28为公差为-6的等差数列的前10项和,代入求和公式可求a1,而a4+a6+a8+…+a48+a50表示a4为首项-4为公差的等差数列前24项和,再由等差数列的求和公式代入a1计算可得.
解答 解:∵{an}是公差为-2的等差数列,
∴a1+a4+a7+…+a25+a28为公差为-6的等差数列的前10项和,
∴10a1+$\frac{10×9}{2}$×(-6)=10a1-270=90,解得a1=36
而a4+a6+a8+…+a48+a50表示a4为首项-4为公差的等差数列前24项和,
∴a4+a6+a8+…+a48+a50=24a4+$\frac{24×23}{2}$×(-4)
=24(a1-6)+$\frac{24×23}{2}$×(-4)
=24×30+$\frac{24×23}{2}$×(-4)
=-384
故答案为:-384
点评 本题考查等差数列的求和公式和等差数列的性质,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.函数y=$\frac{\sqrt{9-{x}^{2}}}{|x+4|+|x-3|}$( )
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既不是奇函数,又不是偶函数 |
 如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
 的值
的值 ,b=2,求△ABC的面积S.
,b=2,求△ABC的面积S.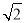 的像和B中元素-1的原像.
的像和B中元素-1的原像.