题目内容
16.已知集合A={y|y=2x+2,x∈[-1,2]},B={x|y=lg[(x-m)2-9]}.(1)若m=3,求(∁RA)∩(∁RB);
(2)若A∩B=∅,求实数m的取值范围.
分析 分别求解函数的值域和定义域化简集合A,B.
(1)把m=3代入集合B,然后利用补集与交集运算得答案;
(2)由A∩B=∅,得$\left\{\begin{array}{l}{m-3≤\frac{5}{2}}\\{m+3≥6}\end{array}\right.$,求解不等式组得答案.
解答 解:A={y|y=2x+2,x∈[-1,2]}=[$\frac{5}{2},6$],
由(x-m)2-9>0,得x<m-3或x>m+3.
∴B={x|y=lg[(x-m)2-9]}=(-∞,m-3)∪(m+3,+∞).
(1)若m=3,则B=(-∞,0)∪(6,+∞).
∁RA=($-∞,\frac{5}{2}$)∪(6,+∞),∁RB=[0,6].
∴(∁RA)∩(∁RB)=[0,$\frac{5}{2}$);
(2)若A∩B=∅,则$\left\{\begin{array}{l}{m-3≤\frac{5}{2}}\\{m+3≥6}\end{array}\right.$,解得:3$≤m≤\frac{11}{2}$.
点评 本题考查交、并、补集的运算,考查了函数的定义域及其值域的求法,是基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.函数y=$\frac{\sqrt{9-{x}^{2}}}{|x+4|+|x-3|}$( )
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既不是奇函数,又不是偶函数 |
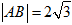 ,则圆C的内接正三角形的面积为( )
,则圆C的内接正三角形的面积为( )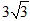 D.
D.