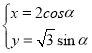题目内容
【题目】已知点(1,e),(e,![]() )在椭圆上C:
)在椭圆上C:![]() 1(a>b>0),其中e为椭圆的离心率.
1(a>b>0),其中e为椭圆的离心率.
(1)求椭圆C的方程;
(2)直线l经过C的上顶点且l与抛物线M:y2=4x交于P,Q两点,F为椭圆的左焦点,直线FP,FQ与M分别交于点D(异于点P),E(异于点Q),证明:直线DE的斜率为定值.
【答案】(1)![]() y2=1;(2)证明见解析
y2=1;(2)证明见解析
【解析】
(1)由椭圆过两个点及e与a,b,c之间的关系求出a,b的值,进而求出椭圆的方程;
(2)由题意可得直线l的斜率存在且不为0,设直线PF的方程与抛物线联立求出两根之和及两根之积,可得点D的坐标,同理可得E的坐标,求出直线DE的斜率可得为定值.
解:(1)由题意可得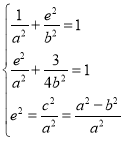 解得:a2=2,b2=1,
解得:a2=2,b2=1,
所以椭圆的方程为:![]() y2=1;
y2=1;
(2)证明:由题意可得直线l的斜率存在且不为0,设直线l的方程为:y=kx+1,设P(x1,y1),Q(x2,y2),
联立直线l与抛物线的方程![]() ,整理可得:
,整理可得:![]() y2﹣y+1=0,△=1﹣k>0即k<1,且k≠0,
y2﹣y+1=0,△=1﹣k>0即k<1,且k≠0,
y1+y2![]() ,y1y2
,y1y2![]() ,
,
由(1)可得左焦点F(﹣1,0),所以直线FP的方程为:y![]() (x+1),
(x+1),
联立直线PF与抛物线的方程: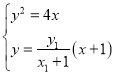 整理可得:y2
整理可得:y2![]() y+4=0,所以y1yD=4,所以yD
y+4=0,所以y1yD=4,所以yD![]() ,
,
所以D的坐标(![]() ,
,![]() ),
),
同理可得:E的坐标(![]() ,
,![]() ),
),
所以kDE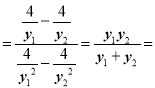 1,
1,
所以可证得直线DE的斜率为定值1.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目