题目内容
【题目】已知正方体![]() 的棱长为
的棱长为![]() 为
为![]() 的中点,下列说法中正确的是( )
的中点,下列说法中正确的是( )
A.![]() 与
与![]() 所成的角大于
所成的角大于![]()
B.点![]() 到平面
到平面![]() 的距离为1
的距离为1
C.三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
【答案】D
【解析】
对于A选项,取![]() 的中点为
的中点为![]() ,可得
,可得![]() ,则
,则![]() 为
为![]() 与
与![]() 所成的角,结合余弦定理即可判断;
所成的角,结合余弦定理即可判断;
对于B选项,求出四棱锥![]() 的所有棱长,从而可得四棱锥
的所有棱长,从而可得四棱锥![]() 的高即为点
的高即为点![]() 到平面
到平面![]() 的距离;
的距离;
对于C选项,可判断三棱锥![]() 的外接球即四棱锥
的外接球即四棱锥![]() 的外接球,根据勾股定理可求出四棱锥
的外接球,根据勾股定理可求出四棱锥![]() 的外接球半径,再根据球的表面积公式即可判断;
的外接球半径,再根据球的表面积公式即可判断;
对于D选项,设![]() 交平面
交平面![]() 于点
于点![]() ,通过线面垂直的判定定理,可推出
,通过线面垂直的判定定理,可推出![]() ,从而可找出直线
,从而可找出直线![]() 与平面
与平面![]() 所成的角,再利用余弦定理即可求得直线
所成的角,再利用余弦定理即可求得直线![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
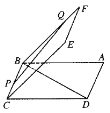
解:如图,正方体![]() 的棱长为
的棱长为![]() 为
为![]() 的中点,
的中点,
对于![]() ,取
,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
则![]() ,则
,则![]() 与
与![]() 所成的角即为
所成的角即为![]() 与
与![]() 所成的角,即为
所成的角,即为![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
由余弦定理得:![]() ,
,
即![]() ,而异面直线夹角为
,而异面直线夹角为![]() ,即
,即![]() ,
,
所以![]() ,故A不正确;
,故A不正确;
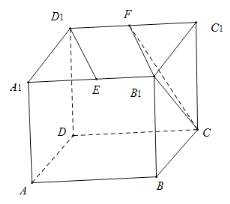
连接![]() ,
,
因为![]() 为矩形,且
为矩形,且![]() ,
,![]() ,
,![]() ,
,
则四棱锥![]() 的顶点
的顶点![]() 投影在底面
投影在底面![]() 的中心,即底面
的中心,即底面![]() 对角线的中点,
对角线的中点,
而底面![]() 的对角线为:
的对角线为:![]() ,
,
则四棱锥![]() 的高为:
的高为:![]() ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,故B不正确;
,故B不正确;
由图可知,![]() 、
、![]() 、
、![]() 、
、![]() 的四点共面,
的四点共面,
所以三棱锥![]() 的外接球即四棱锥
的外接球即四棱锥![]() 的外接球,
的外接球,
设四棱锥![]() 的外接球半径为
的外接球半径为![]() ,
,
则![]() ,解得
,解得![]() ,
,
则三棱锥![]() 的外接球表面积
的外接球表面积![]() ,故C不正确;
,故C不正确;
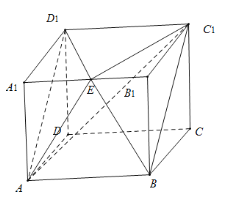
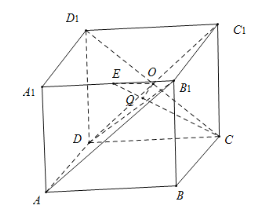
连接![]() ,其中
,其中![]() 与
与![]() 交于点
交于点![]() ,
,
![]() 交平面
交平面![]() 于点
于点![]() ,连接
,连接![]() ,
,
由于![]() 四点共面,平面
四点共面,平面![]() 在平面
在平面![]() 内,
内,
则直线![]() 与平面
与平面![]() 所成的角即为直线
所成的角即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
因为正方体,则![]() ,
,
而![]() 平面
平面![]() ,则
,则![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
则![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
在![]() 中,
中,![]() ,
,
则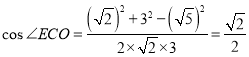 ,得
,得![]() ,
,
所以在![]() 中,
中,![]() ,则
,则![]() ,
,
即:直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,故D正确.
,故D正确.
故选:D.

【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.