题目内容
已知函数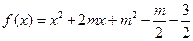 ,当
,当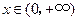 时,
时,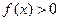 ,求
,求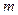 的取值范围.
的取值范围.
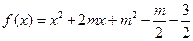 ,当
,当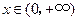 时,
时,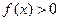 ,求
,求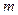 的取值范围.
的取值范围.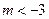 或
或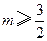
可分两种情况处理,即分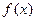 无零点和有零点.
无零点和有零点.
⑴当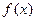 无零点时,
无零点时,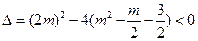 ,解得有
,解得有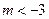 ,
,
 当
当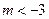 时,对于一切实数
时,对于一切实数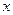 有
有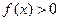 .当然
.当然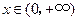 有
有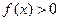 .
.
⑵当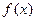 有零点时,且又
有零点时,且又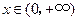 时,
时,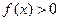 .
.
两个零点必落在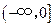 内.
内.
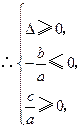
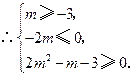
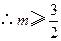 .
.
综上⑴⑵可知当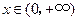 时,
时,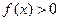 ,
, 的取值范围是
的取值范围是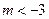 或
或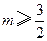 .
.
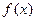 无零点和有零点.
无零点和有零点.⑴当
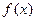 无零点时,
无零点时,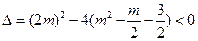 ,解得有
,解得有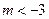 ,
, 当
当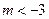 时,对于一切实数
时,对于一切实数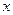 有
有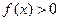 .当然
.当然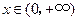 有
有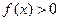 .
.⑵当
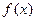 有零点时,且又
有零点时,且又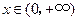 时,
时,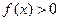 .
.两个零点必落在
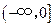 内.
内.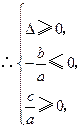
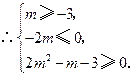
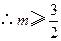 .
.综上⑴⑵可知当
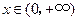 时,
时,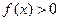 ,
,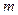 的取值范围是
的取值范围是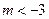 或
或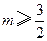 .
.
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 在
在 上是增函数。
上是增函数。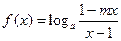
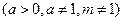
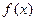 在
在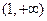 上的单调性,并给出证明;
上的单调性,并给出证明;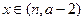 Í
Í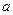 与
与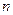
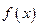 满足
满足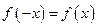 ,如果函数
,如果函数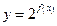 在
在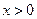 时是增函数,则在
时是增函数,则在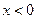 时,是增函数还是减函数?试证明.
时,是增函数还是减函数?试证明.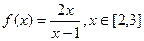 的最大值和最小值。
的最大值和最小值。 ,都有
,都有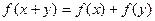 ,且
,且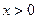 时,f(x)<0,f(1)=-2.
时,f(x)<0,f(1)=-2.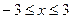 时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
时,f(x)是否有最值?如果有求出最值;如果没有,说出理由. )=0,当x>-
)=0,当x>-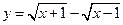 的值域为( )
的值域为( )


