题目内容
求函数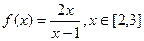 的最大值和最小值。
的最大值和最小值。
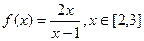 的最大值和最小值。
的最大值和最小值。最大值为4;最小值为3
任取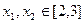 ,且
,且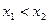 ,则
,则
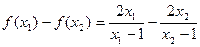
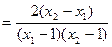
由于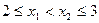 ,
,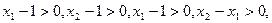
所以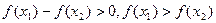 ,因此函数
,因此函数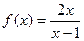 在
在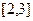 上是减函数
上是减函数
因此, ,函数
,函数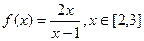 取得最大值为4
取得最大值为4
 ,函数
,函数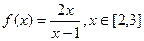 取得最小值为3
取得最小值为3
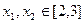 ,且
,且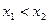 ,则
,则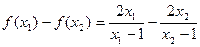
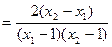
由于
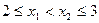 ,
,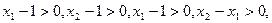
所以
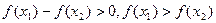 ,因此函数
,因此函数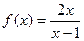 在
在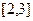 上是减函数
上是减函数因此,
 ,函数
,函数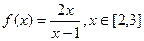 取得最大值为4
取得最大值为4 ,函数
,函数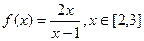 取得最小值为3
取得最小值为3
练习册系列答案
相关题目
题目内容
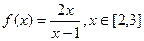 的最大值和最小值。
的最大值和最小值。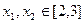 ,且
,且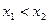 ,则
,则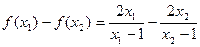
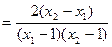
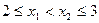 ,
,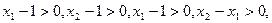
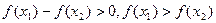 ,因此函数
,因此函数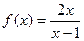 在
在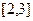 上是减函数
上是减函数 ,函数
,函数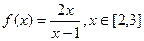 取得最大值为4
取得最大值为4 ,函数
,函数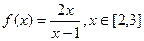 取得最小值为3
取得最小值为3