题目内容
已知函数f(x)的定义域为R,且对m、n∈R,恒有f(m+n)=f(m)+f(n)-1,且f(- )=0,当x>-
)=0,当x>- 时,f(x)>0.
时,f(x)>0.
(1)求证:f(x)是单调递增函数;
(2)试举出具有这种性质的一个函数,并加以验证.
 )=0,当x>-
)=0,当x>- 时,f(x)>0.
时,f(x)>0. (1)求证:f(x)是单调递增函数;
(2)试举出具有这种性质的一个函数,并加以验证.
(1)证明略,(2)f(x)=2x+1
设x1<x2,则x2-x1- >-
>- ,由题意f(x2-x1-
,由题意f(x2-x1- )>0,
)>0,
∵f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)+f(x1)-1-f(x1)
=f(x2-x1)-1=f(x2-x1)+f(- )-1=f[(x2-x1)-
)-1=f[(x2-x1)- ]>0,
]>0,
∴f(x)是单调递增函数.
(2)解: f(x)=2x+1。 验证过程略.
 >-
>- ,由题意f(x2-x1-
,由题意f(x2-x1- )>0,
)>0,∵f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)+f(x1)-1-f(x1)
=f(x2-x1)-1=f(x2-x1)+f(-
 )-1=f[(x2-x1)-
)-1=f[(x2-x1)- ]>0,
]>0,∴f(x)是单调递增函数.
(2)解: f(x)=2x+1。 验证过程略.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
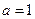 时,证明函数
时,证明函数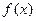 只有一个零点;
只有一个零点;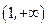 上是减函数,求实数
上是减函数,求实数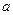 的取值范围
的取值范围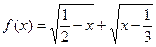 的最大值为
的最大值为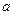 ,最小值为
,最小值为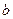 ,则
,则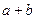 的值是( )
的值是( )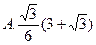
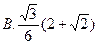
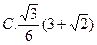
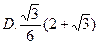
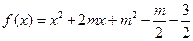 ,当
,当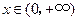 时,
时,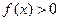 ,求
,求 的取值范围.
的取值范围.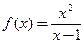 (
(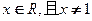 )的单调递增区间是______________________.
)的单调递增区间是______________________.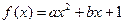 (
( 为实数),
为实数),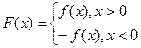
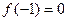 ,且函数
,且函数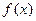 的值域为
的值域为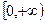 ,求
,求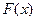 的解析式;
的解析式;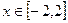 时,
时,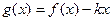 是单调函数,求实数k的取值范围;(3)设
是单调函数,求实数k的取值范围;(3)设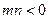 ,
,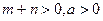 且
且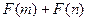 能否大于零?
能否大于零?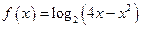 的单调递减区间是( )
的单调递减区间是( )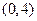 ;
;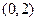 ;
;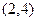 ;
;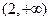

 ,
, ,
,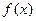 是R上的单调函数且对任意的实数都有
是R上的单调函数且对任意的实数都有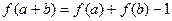 .
.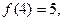 则不等式
则不等式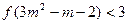 的解集为______________
的解集为______________