题目内容
12.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)及内部面积为S=πab,A1,A2是长轴的两个顶点,B1,B2是短轴的两个顶点,在椭圆上或椭圆内部随机取一点 P,给出下列命题:①△PA1A2为钝角三角形的概率为1;
②△PB1B2为钝角三角形的概率为$\frac{b}{a}$;
③△PA1A2为钝角三角形的概率为$\frac{b}{a}$;
④△PB1B2为锐角三角形的概率为$\frac{a-b}{a}$.
其中正确的命题有①②④.(填上你认为所有正确的命题序号)
分析 分别以短轴两个顶点为直径的两个端点作圆O,以长轴两个顶点为直径的两个端点作圆O′,利用几何概型概率的计算公式,数形结合即得结论.
解答 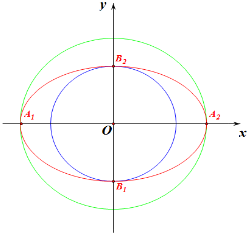 解:如图,以短轴两个顶点为直径的两个端点作圆O,
解:如图,以短轴两个顶点为直径的两个端点作圆O,
则圆O的面积为:πb2.
易得当点P位于圆O内(含边界)时,△PB1B2为钝角三角形,
∴△PB1B2为钝角三角形的概率为:$\frac{π{b}^{2}}{πab}$=$\frac{b}{a}$,
当点P位于圆O外、椭圆内(含边界)时,△PB1B2为锐角三角形,
∴△PB1B2为锐角三角形的概率为:1-$\frac{π{b}^{2}}{πab}$=1-$\frac{b}{a}$=$\frac{a-b}{a}$,
以长轴两个顶点为直径的两个端点作圆O′,
则在椭圆上或椭圆内部随机取一点P,△PA1A2为钝角三角形,
∴△PA1A2为钝角三角形的概率为1,
故答案为:①②④.
点评 本题以椭圆为载体,考查几何概型概率的计算,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
19.下表是某单位在2014年1-5月份用水量(单位:百吨)的一组数据:
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0.05,视为“预测可靠”,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
(2)从这5个月中任取2个月的用水量,求所取2个月的用水灵之和不超过7(单位:百吨)的概率.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 用水量y | 2.5 | 3 | 4 | 4.5 | 5.2 |
(2)从这5个月中任取2个月的用水量,求所取2个月的用水灵之和不超过7(单位:百吨)的概率.
7.经过椭圆x2+2y2=2的一个焦点作倾斜角为45°的直线l,交椭圆于M,N两点,设O为坐标原点,则$\overrightarrow{OM}$•$\overrightarrow{ON}$等于( )
| A. | -3 | B. | ±$\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
4.已知椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的两个焦点为F1,F2,P为椭圆上一点,且PF1⊥PF2,则|PF1|•|PF2|的值为( )
| A. | 48 | B. | 24 | C. | 36 | D. | 25 |
1.b=-1是直线y=x+b过抛物线y2=4x焦点的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
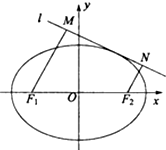 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.