Question

【题目】已知函数f（x）=2x2﹣3x+1， ，（A≠0）
（1）当0≤x≤ 时，求y=f（sinx）的最大值；
（2）若对任意的x1∈[0，3]，总存在x2∈[0，3]，使f（x1）=g（x2）成立，求实数A的取值范围；
（3）问a取何值时，方程f（sinx）=a﹣sinx在[0，2π）上有两解？

Answer 1

【答案】
（1）解：y=f（sinx）=2sin2x﹣3sinx+1设t=sinx，x ，则0≤t≤1

∴

∴当t=0时，ymax=1

（2）解：当x1∈[0，3]∴f（x1）值域为

当x2∈[0，3]时，则 有

② 当A＞0时，g（x2）值域为

②当A＜0时，g（x2）值域为

而依据题意有f（x1）的值域是g（x2）值域的子集

则 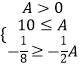或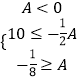

∴A≥10或A≤﹣20

（3）解：2sin2x﹣3sinx+1=a﹣sinx化为2sin2x﹣2sinx+1=a在[0，2π]上有两解

换t=sinx则2t2﹣2t+1=a在[﹣1，1]上解的情况如下：

① 当在（﹣1，1）上只有一个解或相等解，x有两解（5﹣a）（1﹣a）≤0或△=0

∴a∈[1，5]或

②当t=﹣1时，x有惟一解

③当t=1时，x有惟一解

故a∈（1，5）∪{ }

【解析】（1）由已知可得，y=f（sinx）=2sin2x﹣3sinx+1设t=sinx，由x 可得0≤t≤1，从而可得关于 t的函数 ，结合二次函数的性质可求（2）依据题意有f（x1）的值域是g（x2）值域的子集，要求 A的取值范围，可先求f（x1）值域，然后分①当A＞0时，g（x2）值域②当A＜0时，g（x2）值域，建立关于 A的不等式可求A 的范围．（3）2sin2x﹣3sinx+1=a﹣sinx化为2sin2x﹣2sinx+1=a在[0，2π]上有两解令t=sinx则2t2﹣2t+1=a在[﹣1，1]上解的情况可结合两函数图象的交点情况讨论．
【考点精析】通过灵活运用二次函数的性质和三角函数的最值，掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减；函数，当时，取得最小值为；当时，取得最大值为，则，，即可以解答此题．