题目内容
12.对任意两个非零的平面向量$\overrightarrow a$和$\overrightarrow b$,定义$\overrightarrow a*\overrightarrow b=\frac{\overrightarrow a•\overrightarrow b}{\overrightarrow b•\overrightarrow b}$;若平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$|{\overrightarrow a}|>|{\overrightarrow b}|>0$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ∈(0,$\frac{π}{4}$),且$\overrightarrow a*\overrightarrow b,\overrightarrow b*\overrightarrow a$都在集合{$\frac{n}{2}$|n∈Z}中,则$\overrightarrow a*\overrightarrow b$=( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
分析 先求出$\overrightarrow{a}$﹡$\overrightarrow{b}$=$\frac{|\overrightarrow{a}||\overrightarrow{b}|cosθ}{|b{|}^{2}}$=$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}cosθ$=$\frac{n}{2}$,n∈z,$\overrightarrow{b}﹡\overrightarrow{a}=\frac{m}{2},m∈z$再由$co{s}^{2}θ=\frac{nm}{4}∈(\frac{1}{2},1)$ 故 n=3,m=1 从而求出答案.
解答 解:∵$\overrightarrow{a}﹡\overrightarrow{b}=\frac{\overrightarrow{a}•\overrightarrow{b}}{\overrightarrow{b}•\overrightarrow{b}}=\frac{|\overrightarrow{a}\overrightarrow{||b}|cosθ}{|\overrightarrow{b}{|}^{2}}=\frac{|\overrightarrow{a}|}{\overrightarrow{|b}|}cosθ$=$\frac{n}{2}$,n∈z,
同理可得:$\overrightarrow{b}﹡\overrightarrow{a}=\frac{m}{2},\\;\\;m∈z$. m∈z.
再由$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ∈(0,$\frac{π}{4}$),知$co{s}^{2}θ=\frac{nm}{4}∈(\frac{1}{2},1)$,故mn=3,m,n∈z.
∵$|\overrightarrow{a}|>|\overrightarrow{b}|>0$
∴$0<\overrightarrow{b}﹡\overrightarrow{a}=\frac{m}{2}<1$
∴m=1,n=3
∴$\overrightarrow{a}﹡\overrightarrow{b}=\frac{3}{2}$
故答案为B.
点评 本题主要考查两个向量的数量积的定义,求得 m=1,n=3,是解题的关键,属于中档题.

| A. | {0} | B. | {0,1} | C. | {0,1,2} | D. | {0,1,2,4} |
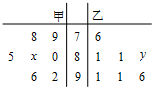 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 7 | C. | 9 | D. | 168 |
| A. | 若ξ-B(4,0.25),则Eξ=1 | |
| B. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0” | |
| C. | 从匀速传递的产品生产线上,检查人员每隔5分钟从中抽出一件产品检查,这样的抽样是系统抽样 | |
| D. | 10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,这组数据的中位数与众数相等 |
 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口E是AB的中点,F,G分别落在AD,BC上,且AB=20m,AD=10$\sqrt{3}$m,设∠GEB=θ. 如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.
如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.