题目内容
16.若复数z=a+bi(i为虚数单位,a,b∈R)在复平面内对应点为Z(a,b),O为坐标原点,将实轴非负半轴绕点O逆时针旋转到OZ,转过的最小角叫复数z的辐角主值,记作arg(z),则arg($\frac{2}{1-i}$)的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
分析 由复数代数形式的乘除运算化简,求出$\frac{2}{1-i}$在复平面内点的坐标得答案.
解答 解:由$\frac{2}{1-i}$=$\frac{2(1+i)}{(1-i)(1+i)}=\frac{2(1+i)}{2}=1+i$,
∴复数$\frac{2}{1-i}$在复平面内对应点的坐标为(1,1),
则arg($\frac{2}{1-i}$)的值为$\frac{π}{4}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数z的辐角主值的概念,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.若某几何体的三视图如图所示,则此几何体的体积是( )
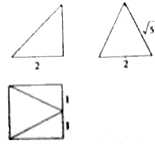

| A. | 4$\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
1.在直角坐标平面xoy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为$\frac{3}{4}$,则抛物线C的方程为( )
| A. | x2=$\frac{1}{2}$y | B. | x2=y | C. | x2=2y | D. | x2=4y |
5.已知集合A={0,1,2,3,4},集合B={y|y=$\sqrt{x}$,x∈A}.则集合A∩B=( )
| A. | {0} | B. | {0,1} | C. | {0,1,2} | D. | {0,1,2,4} |
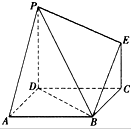 图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2
图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2