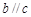题目内容
(本小题满分12分)
正方体ABCD-A1B1C1D1中,E、G分别是BC、C1D1的中点,如图所示.
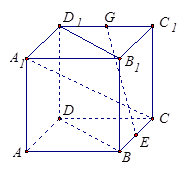
(1)求证:BD⊥A1C;
(2)求证:EG∥平面BB1D1D.
正方体ABCD-A1B1C1D1中,E、G分别是BC、C1D1的中点,如图所示.

(1)求证:BD⊥A1C;
(2)求证:EG∥平面BB1D1D.
(1)证明: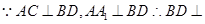 平面
平面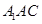
 (2)证明:取BD中点F,连接
(2)证明:取BD中点F,连接
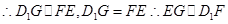
 平面
平面
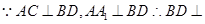 平面
平面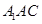
 (2)证明:取BD中点F,连接
(2)证明:取BD中点F,连接
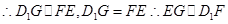
 平面
平面
试题分析:(1)连接AC
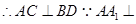 平面
平面
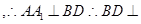 平面
平面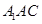 ,
,
(2)取BD的中点F,连接EF,D1F.
∵E为BC的中点,
∴EF为△BCD的中位线,
则EF∥DC,且EF=
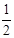 CD.
CD.∵G为C1D1的中点,
∴D1G∥CD且D1G=
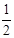 CD,
CD,∴EF∥D1G且EF=D1G,
∴四边形EFD1G为平行四边形,
∴D1F∥EG,而D1F?平面BDD1B1,
EG?平面BDD1B1,
∴EG∥平面BB1D1D.
点评:本题还可用空间向量来证明

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由. ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
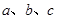 及平面
及平面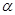 ,它们具备下列哪组条件时,有
,它们具备下列哪组条件时,有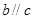 成立( )
成立( )
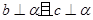
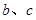 和
和
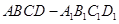 中,
中,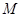 、
、 分别是
分别是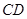 、
、 的中点,则异面直线
的中点,则异面直线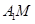 与
与 所成的角的大小是____________.
所成的角的大小是____________.
 ,其中m∥n,那么在平面
,其中m∥n,那么在平面 的中线AF与中位线DE相交于G,已知
的中线AF与中位线DE相交于G,已知 是
是 绕边DE旋转过程中的一个图形,给出四个命题:
绕边DE旋转过程中的一个图形,给出四个命题: 在
在 上的射影在线段
上的射影在线段 上;
上; ;
; 的体积有最大值;
的体积有最大值;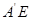 与
与 不可能垂直.
不可能垂直.
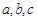 是空间三条直线,
是空间三条直线,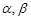 是空间两个平面,则下列命题中,逆命题不正确的是( )
是空间两个平面,则下列命题中,逆命题不正确的是( )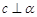 时,若
时,若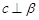 ,则
,则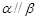
 时,若
时,若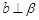 ,则
,则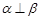
 且
且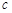 是
是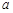 在
在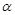 内的射影时,若
内的射影时,若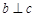 ,则
,则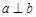
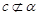 时,若
时,若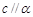 ,则
,则