题目内容
(本题满分12分)如图,四棱锥P—ABCD的底面是矩形,PA⊥面ABCD,PA=2 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.

(1)求EF的长;
(2)证明:EF⊥PC.
 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
(1)求EF的长;
(2)证明:EF⊥PC.
(1)6 (2)见解析
试题分析:(1)以A为原点,
 ,
, ,
, 分别为x,y,z轴建立直角坐标系,…………2分
分别为x,y,z轴建立直角坐标系,…………2分由条件知:AF=2,…………3分
∴F(0,2,0),P(0,0,2
 ),C(8,6,0).…4分
),C(8,6,0).…4分从而E(4,3,
 ),∴EF=
),∴EF=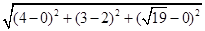 =6.…………6分
=6.…………6分(2)证明:
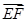 =(-4,-1,-
=(-4,-1,- ),
),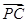 =(8,6,-2
=(8,6,-2 ),…………8分
),…………8分∵
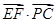 =-4×8+(-1)×6+(-
=-4×8+(-1)×6+(- )×(-2
)×(-2 )=0,…………10分
)=0,…………10分∴EF⊥PC.…………12分
点评:向量法求解立体题目比几何法思路简单明了

练习册系列答案
相关题目
 平面ABCD,
平面ABCD, ,BC=1,E为CD的中点,PC与平面ABCD成
,BC=1,E为CD的中点,PC与平面ABCD成 角。
角。

 //平面
//平面 ,AB、CD是夹在
,AB、CD是夹在 ,求证:
,求证: .
. 、
、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则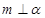
 ,
, ,则
,则 是直线,
是直线, ,
, 是两个不同的平面,下列选项正确的是( )
是两个不同的平面,下列选项正确的是( ) ⊥
⊥ 、
、 ,两个不同平面
,两个不同平面 、
、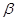 ,给出下列命题:
,给出下列命题:
 ,则
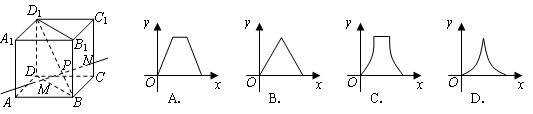
,则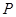 在正方体
在正方体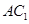 的对角线
的对角线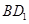 上.过点
上.过点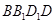 的直线,与正方体表面相交于
的直线,与正方体表面相交于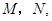 设
设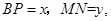 则函数
则函数 的图象大致是( )
的图象大致是( )