题目内容

在递增的等差数列中，已知a3+a6+a9=12，a3•a6•a9=28，则an为（　　）
A．n-2B．16-nC．n-2或16-nD．2-n
设等差数列的公差为d，可得d＞0
由等差数列的性质可得a3+a6+a9=3a6=12，
∴a6=4，
∴（4-3d）×4×（4+3d）=28，
解得d=1，或d=-1（舍去），
∴an=a6+（n-6）d=4+（n-6）=n-2
故选：A
练习册系列答案
相关题目
等差数列{an}中，若a8=
4
3
，则数列{an}的前15项的和是（　　）
A．10B．20C．30D．40
若等差数列的首项是-24，且从第10项开始大于零，则公差d的取值范围是（　　）
A．d＞
8
3
B．d＜3C．
8
3
≤d＜3		D．
8
3
＜d≤3
等差数列{an}的前n项和为Sn，a1=1+
2
，S3=9+3
2
．
（1）求数列{an}的通项an与前n项和为Sn；
（2）设bn=
Sn
n
（n∈N+），求证：数列{bn}中任意不同的三项都不可能成为等比数列．
等差数列{an}中，a3+a4+a5+a6+a7=450，求a2+a8=（　　）
A．180B．45C．75D．300
在等差数列{an}中，a3+a5+a7+a9+a11=20，则a1+a13=______．
等差数列{an}中，a4=1，a8=8，则a12的值是（　　）
A．15B．30C．31D．64
已知数列{an}是一个公差大于0的等差数列，且满足a3a6=55，a2+a7=16
（1）求数列{an}的通项公式；
（2）数列{an}和数列{bn}满足等式an=
b1
2
+
b2
22
+
b3
23
+…+
bn
2n
（n∈N*），求数列{bn}的前n项和Sn．
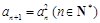数列{an}中，a1 = 3，，则数列的通项公式　   　．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网