题目内容
(12分)已知圆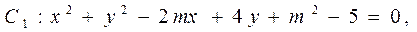 圆
圆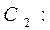
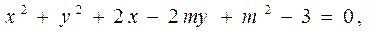 则
则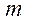 为何值时,
为何值时,
(1) 圆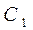 与圆
与圆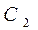 相切;
相切;
(2) 圆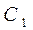 与圆
与圆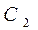 内含。
内含。
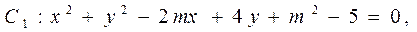 圆
圆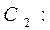
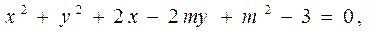 则
则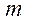 为何值时,
为何值时,(1) 圆
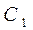 与圆
与圆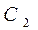 相切;
相切;(2) 圆
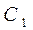 与圆
与圆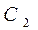 内含。
内含。(1)若圆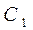 与圆
与圆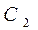 相切,则
相切,则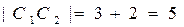 或
或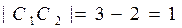
即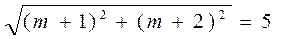 或
或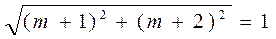
解得: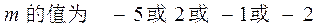
(1) (2)若圆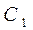 与圆
与圆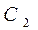 内含,则
内含,则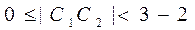
即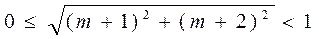
解得: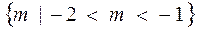
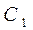 与圆
与圆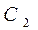 相切,则
相切,则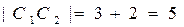 或
或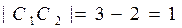
即
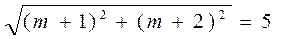 或
或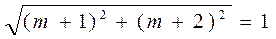
解得:
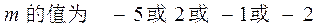
(1) (2)若圆
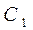 与圆
与圆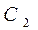 内含,则
内含,则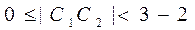
即
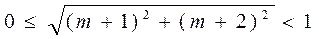
解得:
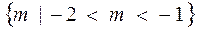
解:将两圆方程化为标准式,得:
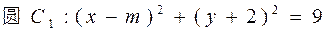
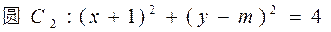 ,
,
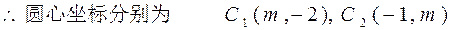
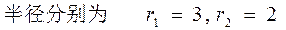
(2) 若圆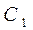 与圆
与圆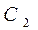 相切,则
相切,则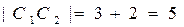 或
或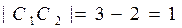
即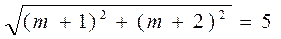 或
或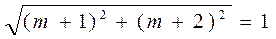
解得: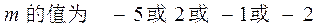
(3) 若圆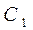 与圆
与圆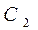 内含,则
内含,则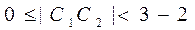
即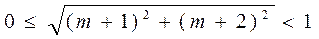
解得: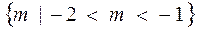
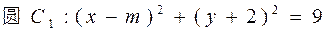
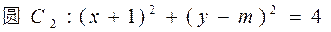 ,
,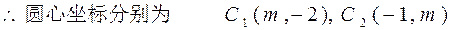
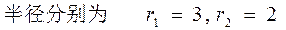
(2) 若圆
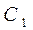 与圆
与圆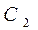 相切,则
相切,则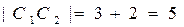 或
或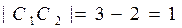
即
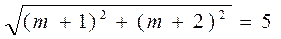 或
或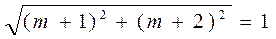
解得:
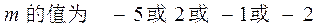
(3) 若圆
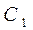 与圆
与圆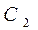 内含,则
内含,则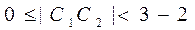
即
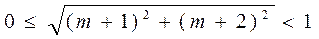
解得:
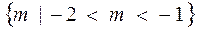

练习册系列答案
相关题目

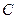 与圆
与圆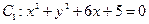 外切,同时与圆
外切,同时与圆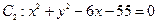 内切.
内切.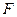 的方程;
的方程;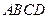 中(如图),
中(如图),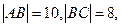
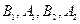 分别是矩形四边的中点,
分别是矩形四边的中点,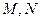 分别是
分别是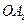 (其中
(其中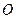 是坐标系原点)
是坐标系原点)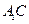 的中点,直线
的中点,直线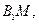
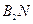 的交点为
的交点为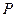 ,证明点
,证明点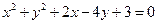 .
.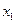 、
、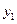 )向该圆引一条切线,切点为M,O为坐标原点,且有
)向该圆引一条切线,切点为M,O为坐标原点,且有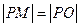 ,求使得
,求使得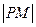 取得最小值的点P的坐标.
取得最小值的点P的坐标.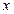 轴同侧的两个圆:动圆
轴同侧的两个圆:动圆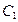 和圆
和圆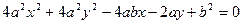 外切(
外切(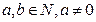 ),且动圆
),且动圆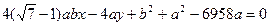 与曲线L有且仅有一个公共点,求
与曲线L有且仅有一个公共点,求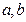 之值。
之值。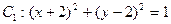 与圆
与圆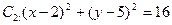 的位置关系是( )
的位置关系是( )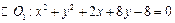 与
与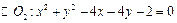 的公共弦长为 .
的公共弦长为 .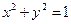 和
和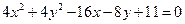 的公切线的斜率是_____________________。
的公切线的斜率是_____________________。