题目内容
已知椭圆 (
( )
) ,M,N是椭圆上关于原点对称的两点,P是椭圆上任意一点,且直线PM,PN的斜率分别为
,M,N是椭圆上关于原点对称的两点,P是椭圆上任意一点,且直线PM,PN的斜率分别为 ,
, =
= ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.  | B. | C. | D. |
C
解析试题分析:设点M(m,n),则N(-m,-n),其中 ,则
,则 ……①
……①
设P(x,y),因为点P在椭圆上,所以 ,即
,即 ………………②
………………②
又k1= ,k2=
,k2= ,因为
,因为 =
= ,所以|
,所以| |=
|= ………………………………③
………………………………③
① ②代入③得:| |=
|= ,即
,即 ,所以
,所以 ,所以
,所以 。
。
考点:本题考查椭圆的基本性质;椭圆的离心率;直线的斜率公式。
点评:本题主要考查了椭圆的应用,考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
椭圆 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )
A. | B. | C. | D. |
椭圆 上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列, 则n的最大值是( )
的等差数列, 则n的最大值是( )
| A.198 | B.199 | C.200 | D.201 |
双曲线 上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
| A.1或13 | B.15 | C.13 | D.1 |
曲线 与曲线
与曲线 的( )
的( )
| A.长轴长相等 | B.短轴长相等 | C.离心率相等 | D.焦距相等 |
椭圆 的焦点为F1和F2 ,点P在椭圆上,如果线段PF1的中点在y轴上,那么︱PF1︱是︱PF2︱
的焦点为F1和F2 ,点P在椭圆上,如果线段PF1的中点在y轴上,那么︱PF1︱是︱PF2︱
| A.3倍 | B.4倍 | C.5倍 | D.7倍 |

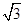


 的两个焦点,过F2的直线交椭圆于点A、B,若
的两个焦点,过F2的直线交椭圆于点A、B,若 ,
,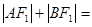 ( )
( ) 


