Question

【题目】若点P（x，y）在圆上，则代数式的最大值是_____．

Answer 1

【答案】1

【解析】

= ，设＝t，＝k，分别求出t与k的最大值，以及取最大值的条件，结果它们取最大值的条件相同，所以t与k都取最大值时，所求代数式取最大值．

∵圆x2+y2+10x+10y+45＝0，即（x+5）2+（y+5）2＝5是以（5，5）为圆心，以为半径的圆，因为代数式＝+，令＝k，＝t，

因为k表示原点O与P点连线的斜率，所以当直线OP与圆相切时，＝，解得k＝或k＝2，所以k的最大值为2，此时联立直线与圆可解得x＝﹣3，y＝﹣6，

因为直线x﹣y﹣t＝0与圆有交点，所以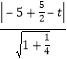 ≤，解得﹣5≤t≤0，

所以t的最大值为0，此时x﹣y＝0，可解得切点为（﹣3，﹣6），

由于k和t取最大值时得条件相同，都是x＝﹣3，y＝﹣6，

所以代数式的最大值为2×+0＝1．

故答案为：1．