题目内容
【题目】已知椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() 右焦点为
右焦点为![]() ,直线
,直线![]() 是椭圆
是椭圆![]() 在点
在点![]() 处的切线.设点
处的切线.设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,且当
,且当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设椭圆![]() 的长轴长等于
的长轴长等于![]() ,当点
,当点![]() 运动时,试判断以
运动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
【答案】(1)![]() (2)以
(2)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
解:(Ⅰ)根据题意,得直线![]() 与
与![]() 轴垂直,
轴垂直,
![]() 当
当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
![]()
![]()
![]()
![]()
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系是相切,证明如下:
的位置关系是相切,证明如下:
![]() 椭圆C的长轴长等于
椭圆C的长轴长等于![]() ,
,
![]()
根据(Ⅰ),得椭圆的标准方程为: ![]() ,
,
设直线![]() 的方程为:
的方程为: ![]() ,
,
则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
联立方程组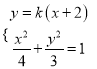 ,消去
,消去![]() ,并整理,得
,并整理,得
![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则
,则
![]()
![]()
因为点![]() ,
,
(ⅰ)当![]() 时,点
时,点![]() 坐标为
坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,此时,以
,此时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切;
相切;
(ⅱ)当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为:
的方程为: ![]() ,
,
![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为 ,
,
![]() ,
,
![]() 以
以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
【解析】试题分析:(Ⅰ)根据题意,结合给定的条件,得到![]() ,然后确定其离心率即可;
,然后确定其离心率即可;
(Ⅱ)设直线![]() 的方程为:
的方程为: ![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
联立方程组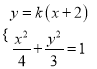 ,消去
,消去![]() ,并整理,得
,并整理,得![]() ,
,
分情况进行讨论,结合直线与圆相切的条件进行判断即可.
试题解析:(Ⅰ)根据题意,得直线![]() 与
与![]() 轴垂直,
轴垂直,
![]() 当
当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
![]()
![]()
![]()
![]()
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系是相切,证明如下:
的位置关系是相切,证明如下:
![]() 椭圆C的长轴长等于
椭圆C的长轴长等于![]() ,
,
![]()
根据(Ⅰ),得椭圆的标准方程为: ![]() ,
,
设直线![]() 的方程为:
的方程为: ![]() ,
,
则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
联立方程组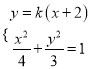 ,消去
,消去![]() ,并整理,得
,并整理,得
![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则
,则
![]()
![]()
因为点![]() ,
,
(ⅰ)当![]() 时,点
时,点![]() 坐标为
坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,此时,以
,此时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切;
相切;
(ⅱ)当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为:
的方程为: ![]() ,
,
![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为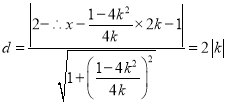 ,
,
![]() ,
,
![]() 以
以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.

练习册系列答案
相关题目