题目内容
函数f(x) 的定义域为R,且对任意x,y∈R 都有f(x+y)=f(x)+f(y),又
当x>0 时,f(x)<0,且f(1)=-2.
(Ⅰ)求证:f(x) 既是奇函数又是R上的减函数;
(Ⅱ)求f(x)在[-3,3]的最大值和最小值.
当x>0 时,f(x)<0,且f(1)=-2.
(Ⅰ)求证:f(x) 既是奇函数又是R上的减函数;
(Ⅱ)求f(x)在[-3,3]的最大值和最小值.
(Ⅰ)见解析(Ⅱ)f(x)在[-3,3]的最大值是6,最小值是-6
本试题主要是考查了函数的奇偶性和单调性的运用。
(1)证明:由f(x+y)=f(x)+f(y)得f[x+(-x)]=f(x)+f(-x)
即f(x)+f(-x)=f(0),故∴f(x)+f(-x)=0即f(-x)=-f(x)即f(x) 是奇函数,并运用定义法证明单调性。
(2)∵f(x)在R上单调递减,
∴在[-3,3]的最大值为f(-3),最小值为f(3)从而得到。
解:(1)证明:由f(x+y)=f(x)+f(y)得f[x+(-x)]=f(x)+f(-x)
即f(x)+f(-x)="f(0)" ………………………(2分)
∴f(0)+f(0)=f(0)即f(0)=0
∴f(x)+f(-x)=0即f(-x)=-f(x)即f(x) 是奇函数………………………(4分)
又任取 且
且
∵则 …………………(6分)
…………………(6分)
∵ ∴
∴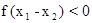
∴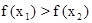 ,f(x)是R上的减函数………………………(8分)
,f(x)是R上的减函数………………………(8分)
(1)解答:∵f(x)在R上单调递减,
∴在[-3,3]的最大值为f(-3),最小值为f(3) ………………(9分)
由f(1)=-2得f(3)=f(1+2)=f(1)+f(1+1)=f(1)+f(1)+f(1)=3f(1)=-6
又f(-3)=-f(3)=6……………(11分)
∴f(x)在[-3,3]的最大值是6,最小值是-6……………………(12分)
(1)证明:由f(x+y)=f(x)+f(y)得f[x+(-x)]=f(x)+f(-x)
即f(x)+f(-x)=f(0),故∴f(x)+f(-x)=0即f(-x)=-f(x)即f(x) 是奇函数,并运用定义法证明单调性。
(2)∵f(x)在R上单调递减,
∴在[-3,3]的最大值为f(-3),最小值为f(3)从而得到。
解:(1)证明:由f(x+y)=f(x)+f(y)得f[x+(-x)]=f(x)+f(-x)
即f(x)+f(-x)="f(0)" ………………………(2分)
∴f(0)+f(0)=f(0)即f(0)=0
∴f(x)+f(-x)=0即f(-x)=-f(x)即f(x) 是奇函数………………………(4分)
又任取
 且
且
∵则
 …………………(6分)
…………………(6分)∵
 ∴
∴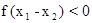
∴
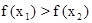 ,f(x)是R上的减函数………………………(8分)
,f(x)是R上的减函数………………………(8分)(1)解答:∵f(x)在R上单调递减,
∴在[-3,3]的最大值为f(-3),最小值为f(3) ………………(9分)
由f(1)=-2得f(3)=f(1+2)=f(1)+f(1+1)=f(1)+f(1)+f(1)=3f(1)=-6
又f(-3)=-f(3)=6……………(11分)
∴f(x)在[-3,3]的最大值是6,最小值是-6……………………(12分)

练习册系列答案
相关题目
 满足:
满足: ,且对于任意的
,且对于任意的 ,都有
,都有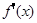 <
< ,则不等式
,则不等式 >
> 的解集为 。
的解集为 。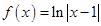 的图像大致是( )
的图像大致是( )
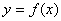 是定义在
是定义在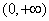 上的减函数,并且满足
上的减函数,并且满足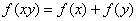 ,
,
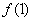 ,
,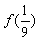 ,
,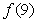 的值,(2)如果
的值,(2)如果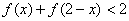 ,求x的取值范围。
,求x的取值范围。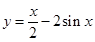 的图象大致是
的图象大致是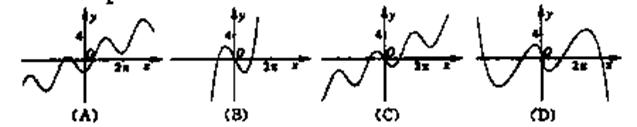
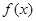 是定义在R上的奇函数,且
是定义在R上的奇函数,且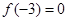 。当
。当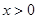 时,有
时,有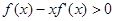 成立,则不等式
成立,则不等式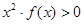 的解集是
的解集是

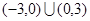
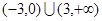
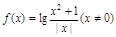 ,有下列命题:
,有下列命题: 轴对称; ②当
轴对称; ②当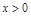 时,
时,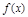 是增函数;当
是增函数;当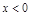 时,
时,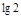 ; ④当
; ④当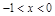 和
和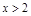 时,
时,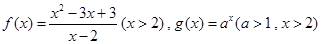 ,若
,若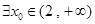 使
使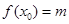 成立,则实数m的取值范围是 ,若
成立,则实数m的取值范围是 ,若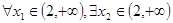 使
使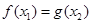 ,则实数a的取值范围是 。
,则实数a的取值范围是 。