题目内容
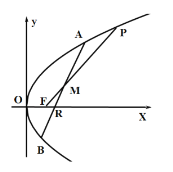
【题目】如图，已知点
，点
均在圆
上，且
，过点
作
的平行线分别交
，
于
两点.
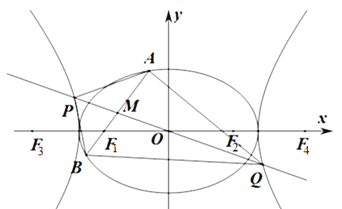
（1）求点
的轨迹方程；
（2）过点
的动直线
与点的轨迹交于
两点．问是否存在常数
，使得
点为定值？若存在，求出的值；若不存在，说明理由．
【答案】（1）
；（2）存在常数
符合题意，理由详见解析.
【解析】
（1）由平面几何的相关性质可得
，则
，即点
的轨迹是以
为焦点的椭圆，再求出椭圆的标准方程即可；
（2）当直线
的斜率存在时，设
，
，
，联立直线方程与椭圆方程，消元列出韦达定理，则
代入计算可得
的值，再计算斜率不存在时的值，即可得解；
解：（1）由
，得
，
由
，得
，所以
.
由
，知
，
所以
，即，
所以，
所以点的轨迹是以为焦点的椭圆.
这里
，
，所以
，
，
则点的轨迹方程为：.
（2）当直线与
轴不垂直时，设，，，
联立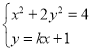
得
，
其判别式
，
所以
，
，
，
所以当时，
，
此时
为定值.
当直线的斜率不存在时，.
综上，存在常数，使得
为定值img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/22/0c62e4d8/SYS202011262207475451781454_DA/SYS202011262207475451781454_DA.037.png" width="22" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />.
练习册系列答案
特高级教师点拨系列答案
相关题目
