题目内容
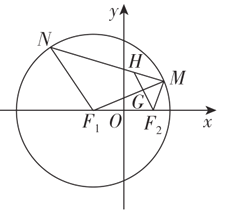
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,且
上的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 是椭圆
是椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
【答案】(1)![]() ,离心率为
,离心率为![]() ;(2)见解析
;(2)见解析
【解析】
(1)由题得关于![]() 的方程组,解之即得椭圆的方程和离心率;(2)由题意可设直线
的方程组,解之即得椭圆的方程和离心率;(2)由题意可设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求出
,求出 ![]() ,
,![]() ;再对
;再对![]() 分类讨论得当点
分类讨论得当点![]() 在椭圆上运动时,以
在椭圆上运动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
(1)由题意可设椭圆![]() 的方程为
的方程为![]() ,
,![]() ;由题意知
;由题意知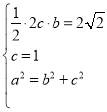 ,
,
解得![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() ,离心率为
,离心率为![]() ;
;
(2)证明:由题意可设直线![]() 的方程为
的方程为![]() ,
,
则点![]() 坐标为
坐标为![]() ,
,![]() 中点
中点![]() 的坐标为
的坐标为![]() ;
;
由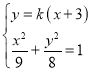 ,得
,得![]() ;
;
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ;
;
因为点![]() 坐标为
坐标为![]() ,当
,当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,
,
此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切;
相切;
当![]() 时,则直线
时,则直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为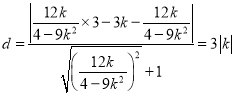 ;
;
又因为![]() ,所以
,所以![]() ,故以
,故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切;
相切;
综上,当点![]() 在椭圆上运动时,以
在椭圆上运动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.

练习册系列答案
相关题目
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.