题目内容
17.求方程:sinx+cosx=1在[0,π]上的解.分析 由两角和的正弦函数可化原方程为$sin(x+\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,结合x的范围可得x的值.
解答 解:原方程可化为$\sqrt{2}sin(x+\frac{π}{4})=1$,
∴$sin(x+\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,
∵x∈[0,π],
∴$x+\frac{π}{4}∈[\frac{π}{4},\frac{5π}{4}]$,
$x+\frac{π}{4}=\frac{π}{4}$或$\frac{3π}{4}$,
解得x=0或$\frac{π}{2}$
点评 本题考查两角和的正弦函数,属基础题.

练习册系列答案
相关题目
17.已知cosx=$\frac{1}{3}$,则cos2x=( )
| A. | $\frac{2}{3}$ | B. | -$\frac{8}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
5.数列{an}满足a1=a2=1,an+2=an+1+an恒成立,则a6=( )
| A. | 8 | B. | 13 | C. | 21 | D. | 5 |
9.${(\root{3}{x}+\frac{1}{x})^n}$的展开式中第5项是常数项,那么这个展开式中系数最大的项为( )
| A. | 第9项 | B. | 第8项 | C. | 第9项和第10项 | D. | 第8项和第9项 |
7.阅读程序框图,任意输入一次x(-1≤x≤1)与y(-1≤y≤1),则能输出数对(x,y)的概率为( )
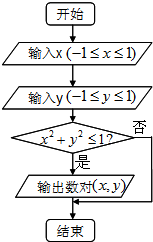

| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |