题目内容
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有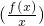 的导数小于零恒成立,则不等式
的导数小于零恒成立,则不等式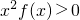 的解集是
的解集是
- A.(一2,0)∪(2,+∞)
- B.(一2,0)∪(0,2)
- C.(-∞,-2)∪(2,+∞)
- D.(-∞,-2)∪(0,2)
D
分析:首先根据商函数求导法则,求出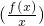 的导数
的导数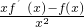 ;然后利用导函数的正负性,判断函数y=
;然后利用导函数的正负性,判断函数y= 在(0,+∞)内单调递减;再由f(2)=0,易得f(x)在(0,+∞)内的正负;最后结合奇函数的图象特征,可得f(x)在(-∞,0)内的正负性.则x2f(x)>0?f(x)>0的解集即可求得.
在(0,+∞)内单调递减;再由f(2)=0,易得f(x)在(0,+∞)内的正负;最后结合奇函数的图象特征,可得f(x)在(-∞,0)内的正负性.则x2f(x)>0?f(x)>0的解集即可求得.
解答:由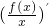 =
=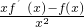
因为当x>0时,有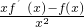 <0恒成立,即[
<0恒成立,即[ ]′<0恒成立,
]′<0恒成立,
∴y= 在(0,+∞)内单调递减,
在(0,+∞)内单调递减,
∵f(2)=0,
∴在(0,2)内恒有f(x)>0;在(2,+∞)内恒有f(x)<0.
又∵f(x)是定义在R上的奇函数,
∴在(-∞,-2)内恒有f(x)>0;在(-2,0)内恒有f(x)<0.
又不等式x2f(x)>0的解集,即不等式f(x)>0的解集.
故答案为:(-∞,-2)∪(0,2).
点评:本题主要考查函数求导法则及函数单调性与导数的关系,判断函数的单调性时,常可利用导函数来判断,注意转化思想的应用.
分析:首先根据商函数求导法则,求出
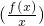 的导数
的导数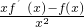 ;然后利用导函数的正负性,判断函数y=
;然后利用导函数的正负性,判断函数y= 在(0,+∞)内单调递减;再由f(2)=0,易得f(x)在(0,+∞)内的正负;最后结合奇函数的图象特征,可得f(x)在(-∞,0)内的正负性.则x2f(x)>0?f(x)>0的解集即可求得.
在(0,+∞)内单调递减;再由f(2)=0,易得f(x)在(0,+∞)内的正负;最后结合奇函数的图象特征,可得f(x)在(-∞,0)内的正负性.则x2f(x)>0?f(x)>0的解集即可求得.解答:由
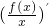 =
=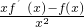
因为当x>0时,有
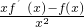 <0恒成立,即[
<0恒成立,即[ ]′<0恒成立,
]′<0恒成立,∴y=
 在(0,+∞)内单调递减,
在(0,+∞)内单调递减,∵f(2)=0,
∴在(0,2)内恒有f(x)>0;在(2,+∞)内恒有f(x)<0.
又∵f(x)是定义在R上的奇函数,
∴在(-∞,-2)内恒有f(x)>0;在(-2,0)内恒有f(x)<0.
又不等式x2f(x)>0的解集,即不等式f(x)>0的解集.
故答案为:(-∞,-2)∪(0,2).
点评:本题主要考查函数求导法则及函数单调性与导数的关系,判断函数的单调性时,常可利用导函数来判断,注意转化思想的应用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |