题目内容
设数列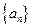 满足关系式:
满足关系式: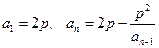 (p是常数).
(p是常数).
(Ⅰ)求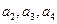 ;
;
(Ⅱ)猜想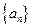 的通项公式,并证明.
的通项公式,并证明.
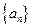 满足关系式:
满足关系式: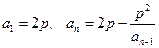 (p是常数).
(p是常数).(Ⅰ)求
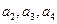 ;
;(Ⅱ)猜想
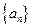 的通项公式,并证明.
的通项公式,并证明. 2°假设
2°假设
 时,命题成立,即
时,命题成立,即 ,则
,则
故
 时,命题仍然成立.
时,命题仍然成立.综上所述:对任何
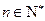 ,均有
,均有 .…………………………12分
.…………………………12分略

练习册系列答案
相关题目
题目内容
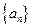 满足关系式:
满足关系式: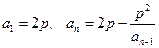 (p是常数).
(p是常数).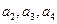 ;
;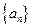 的通项公式,并证明.
的通项公式,并证明. 2°假设
2°假设
 时,命题成立,即
时,命题成立,即 ,则
,则
 时,命题仍然成立.
时,命题仍然成立.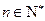 ,均有
,均有 .…………………………12分
.…………………………12分