题目内容
已知点M（0，2），抛物线y2=4x上的动点P到y轴的距离为d，则d+|MP|的最小值为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：抛物线y2=4x的焦点F（1，0），当M，P，F三点共线时，d+|MP|取最小值|MF|-1．
解答：
解：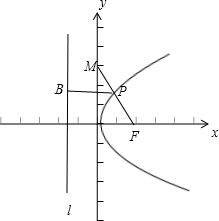
抛物线y2=4x的焦点F（1，0），
如图，d=|PB|-1=|PF|-1，
当M，P，F三点共线时，d+|MP|取最小值，
∴d+|MP|的最小值为：
|MF|-1=
-1=
-1．
故选：B．
抛物线y2=4x的焦点F（1，0），如图，d=|PB|-1=|PF|-1，
当M，P，F三点共线时，d+|MP|取最小值，
∴d+|MP|的最小值为：
|MF|-1=
| (1-0)2+(0-2)2 |
| 5 |
故选：B．
点评：本题考查两线段和的最小值的求法，是基础题，解题时要认真审题，注意抛物线的性质的合理运用．
练习册系列答案
相关题目
下列各组函数f（x）与g（x）的图象相同的是（ ）
A、f（x）=x，g（x）=（
| |||||
| B、f（x）=x2，g（x）=（x+1）2 | |||||
C、f（x）=|x|，g（c）=
| |||||
| D、f（x）=1，g（x）=x0 |
如图，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=1，AB=2，M是PB的中点．