题目内容
已知y=f(x)是奇函数,在(-∞,0)上是增函数,且f(x)>0;求它在(0,+∞)上的单调性及f(x)的符号正负.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:利用函数的奇偶性,得到f(-x)=-f(x),将函数f(x)在(0,+∞)上的问题转化到(-∞,0),利用条件:y=f(x)是奇函数,在(-∞,0)上,f(x)是增函数,且f(x)>0,得到本题结论.
解答:
解:∵函数y=f(x)是奇函数,
∴f(-x)=-f(x).
(1)在(0,+∞)上任取x1,x2,且x1<x2,
∴0>-x1>-x2,
∵函数y=f(x)在(-∞,0)上是增函数,
∴f(-x1)>f(-x2),
∴-f(x1)>-f(x2),
∴f(x2)>f(x1),
∴函数y=f(x)在(0,+∞)上的单调增函数.
(2)当x>0时,-x<0,
∵在(-∞,0)上f(x)>0,
∴f(-x)>0,
∴-f(x)>0,
∴f(x)<0.
∴在(0,+∞)上,数f(x)单调递增且f(x)<0.
∴f(-x)=-f(x).
(1)在(0,+∞)上任取x1,x2,且x1<x2,
∴0>-x1>-x2,
∵函数y=f(x)在(-∞,0)上是增函数,
∴f(-x1)>f(-x2),
∴-f(x1)>-f(x2),
∴f(x2)>f(x1),
∴函数y=f(x)在(0,+∞)上的单调增函数.
(2)当x>0时,-x<0,
∵在(-∞,0)上f(x)>0,
∴f(-x)>0,
∴-f(x)>0,
∴f(x)<0.
∴在(0,+∞)上,数f(x)单调递增且f(x)<0.
点评:本题考查了函数的奇偶性和单调性,本题难度不大,属于基础题.

练习册系列答案
相关题目
下列那个图形可以与空间平行六面体进行类比( )
| A、三角形 | B、梯形 |
| C、平行四边形 | D、矩形 |
已知点P(1,-1)落在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点M(0,2),抛物线y2=4x上的动点P到y轴的距离为d,则d+|MP|的最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
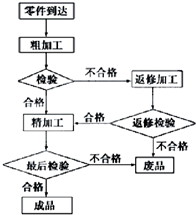 某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了
某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了