题目内容
设两个非零向量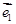 和
和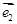 不共线.
不共线.
(1) 如果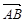 =
=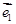 +
+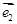 ,
,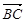 =
=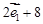
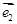 ,
,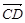 =
=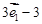
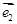 ,求证:
,求证: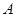 、
、 、
、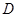 三点共线;
三点共线;
(2) 若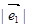 =2,
=2,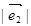 =3,
=3,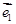 与
与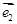 的夹角为
的夹角为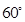 ,是否存在实数
,是否存在实数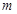 ,使得
,使得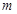
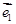
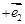 与
与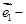
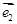 垂直?并说明理由.
垂直?并说明理由.
(1) 证明见解析; (2) 存在实数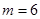 ,使得
,使得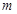
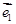
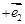 与
与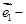
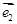 垂直.
垂直.
解析试题分析:(1)证明三点共线,只需证明三点构成的向量中任意两向量共线即可,由向量的运算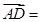
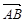 +
+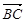 +
+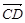
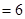
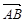 ,所以向量共线,那么三点共线;(2)假设存在实数
,所以向量共线,那么三点共线;(2)假设存在实数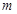 ,使
,使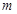
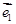
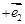 与
与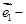
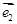 垂直,那么(
垂直,那么(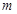
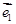
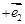 )
) (
(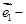
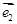 )=
)=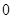 ,又
,又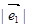 =2,
=2,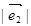 =3,
=3,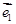 与
与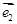 的夹角为
的夹角为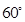 ,将等式展可代入可得关于m的方程
,将等式展可代入可得关于m的方程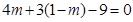 ,得
,得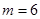 .
.
证明:(1)
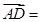
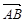 +
+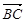 +
+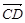 =(
=(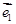 +
+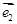 )+(
)+(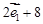
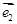 )+(
)+(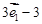
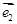 )
)
=6(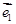 +
+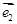 )=6
)=6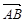 ,
, 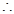
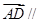
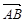 且
且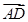 与
与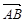 有共同起点.
有共同起点.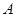 、
、 、
、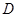 三点共线
三点共线
(2)假设存在实数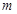 ,使得
,使得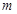
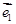
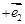 与
与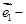
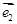 垂直,则(
垂直,则(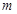
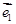
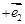 )
) (
(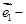
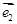 )=
)=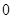
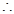
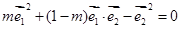

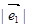 =2,
=2,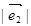 =3,
=3,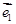 与
与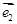 的夹角为
的夹角为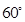
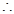
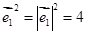 ,
,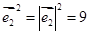 ,
,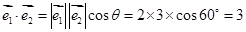

练习册系列答案
相关题目
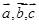 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
. ,且
,且 ,求向量
,求向量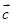 ;
; ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角的正弦值.
的夹角的正弦值. 的终边分别与单位圆交于A、B两点。
的终边分别与单位圆交于A、B两点。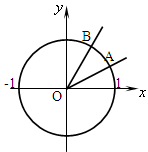
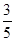 ,点B的横坐标为
,点B的横坐标为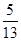 ,求
,求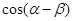 ;
;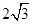 ,-2),
,-2),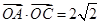 ,求
,求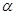
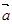 、
、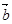 是不共线的两个非零向量.
是不共线的两个非零向量. ,求证:
,求证: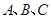 三点共线;
三点共线;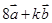 与
与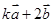 共线,求实数
共线,求实数 的值.
的值.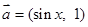 ,
,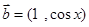 ,函数
,函数 ,
,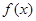 的值域;
的值域; ,且
,且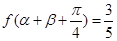 ,
, ,求
,求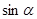 的值。
的值。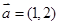 ,
,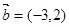 ,当
,当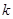 为何值时,
为何值时,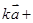
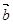 与
与
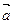 =(2,3),
=(2,3),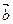 =(
=( ,2),那么
,2),那么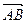 与
与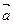 =(2,3)同向,
=(2,3)同向,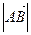 =2
=2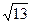 ,则点B的坐标为 .
,则点B的坐标为 .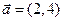 ,
,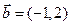 .若
.若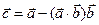 ,则
,则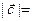 _____________.
_____________.