题目内容
已知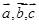 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(Ⅰ)若 ,且
,且 ,求向量
,求向量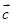 ;
;
(Ⅱ)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角的正弦值.
的夹角的正弦值.
(Ⅰ)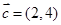 或
或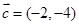 ;(Ⅱ)
;(Ⅱ)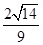 .
.
解析试题分析:(Ⅰ)因为是在坐标前提下解决问题,所以求向量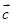 ,即求它的坐标,这样就必须建立关于坐标的方程;(Ⅱ)求
,即求它的坐标,这样就必须建立关于坐标的方程;(Ⅱ)求 与
与 的夹角的正弦值,首先应想到求它们的余弦值,如何求
的夹角的正弦值,首先应想到求它们的余弦值,如何求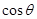 ,还是要建立关于它的方程,可由
,还是要建立关于它的方程,可由 与
与 垂直关系,确立方程来解决问题.
垂直关系,确立方程来解决问题.
试题解析:(Ⅰ)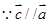 ,可设
,可设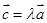 , 1分
, 1分
∴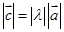 ,
,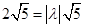 , 2分
, 2分
∴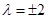 4分
4分
∴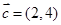 或
或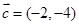 . 6分
. 6分
(Ⅱ)∵ 与
与 垂直,∴
垂直,∴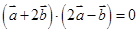 ,即
,即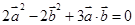 8分
8分
∴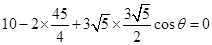 ,∴
,∴ , 10分
, 10分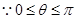
 ,所以
,所以 与
与 的夹角的正弦值
的夹角的正弦值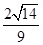 12分
12分
考点:平面向量的坐标运算和向量之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
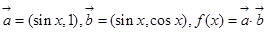
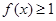 ,求x的范围;
,求x的范围;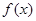 的最大值以及此时x的值.
的最大值以及此时x的值.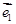 和
和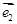 不共线.
不共线.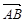 =
=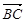 =
=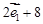
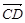 =
=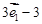
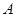 、
、 、
、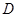 三点共线;
三点共线;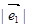 =2,
=2,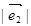 =3,
=3,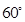 ,是否存在实数
,是否存在实数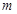 ,使得
,使得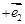 与
与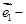
 ,
, 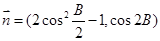 ,且
,且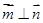 ,
,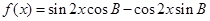 的单调减区间;
的单调减区间;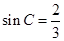 ,求
,求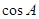 .
. ,点
,点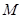 为
为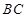 的中点,点
的中点,点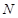 满足
满足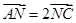 ,点
,点 满足
满足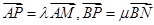 .
.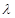 与
与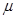 的值;
的值;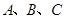 三点坐标分别为
三点坐标分别为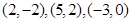 ,求
,求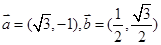
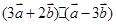 的值;
的值;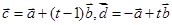 ,且
,且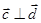 ,求实数t的值.
,求实数t的值.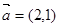 ,
,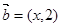 ,若
,若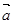 ⊥
⊥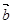 ,则
,则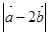 =_________
=_________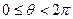 ,已知两个向量
,已知两个向量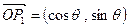 ,
,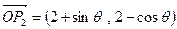 ,则向量
,则向量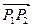 长度的最大值是
长度的最大值是