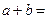题目内容
(本小题12分)设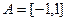 ,
,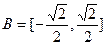 ,函数
,函数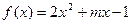 ,
,
(Ⅰ)设不等式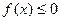 的解集为C,当
的解集为C,当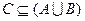 时,求实数
时,求实数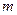 取值范围;
取值范围;
(Ⅱ)若对任意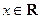 ,都有
,都有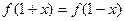 成立,试求
成立,试求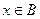 时,
时,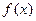 的值
的值 域;
域;
(Ⅲ)设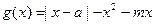
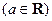 ,求
,求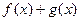 的最
的最 小值.
小值.
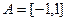 ,
,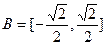 ,函数
,函数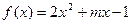 ,
,(Ⅰ)设不等式
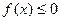 的解集为C,当
的解集为C,当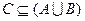 时,求实数
时,求实数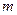 取值范围;
取值范围;(Ⅱ)若对任意
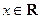 ,都有
,都有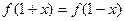 成立,试求
成立,试求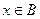 时,
时,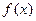 的值
的值 域;
域;(Ⅲ)设
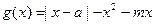
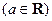 ,求
,求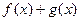 的最
的最 小值.
小值.解:(1)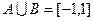 ,因为
,因为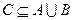 ,二次函数
,二次函数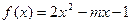 图像
图像
开口向上,且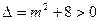 恒成立,故图像始终与
恒成立,故图像始终与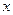 轴有两个交点,由题意,要使这两个
轴有两个交点,由题意,要使这两个
交点横坐标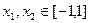 ,当且仅当:
,当且仅当:
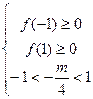 , 解得:
, 解得: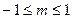

(2)对任意 都有
都有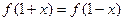 ,所以
,所以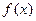 图像关于直线
图像关于直线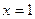 对称,
对称,
所以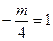 ,得
,得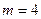 .所以
.所以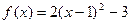 为
为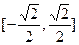 上减函数.
上减函数.
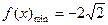 ;
;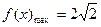 .故
.故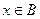 时,
时,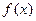 值域为
值域为 .
.
(3)令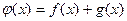 ,则
,则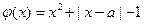
(i)当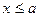 时,
时,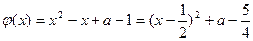 ,
,
当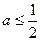 ,则函数
,则函数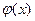 在
在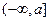 上单调递减,
上单调递减,
从而函数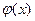 在
在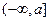 上的最小值为
上的最小值为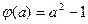 .
.
若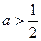 ,则函数
,则函数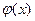 在
在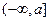 上
上 的最小值为
的最小值为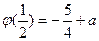 ,且
,且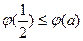 .
.
(ii) 当
当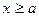 时,函数
时,函数
若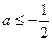 ,则函数
,则函数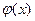 在
在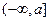 上的最小值为
上的最小值为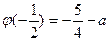 ,且
,且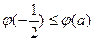
若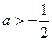 ,则函数
,则函数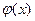 在
在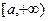 上单调递增,
上单调递增,
从而函数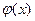 在
在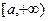 上的最小值为
上的最小值为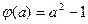 .
.
综上,当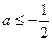 时,函数
时,函数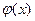 的最小值为
的最小值为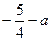
当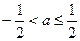 时,函数
时,函数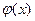 的最小值为
的最小值为
当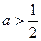 时,函数
时,函数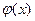 的最小值为
的最小值为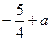
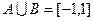 ,因为
,因为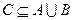 ,二次函数
,二次函数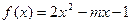 图像
图像开口向上,且
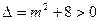 恒成立,故图像始终与
恒成立,故图像始终与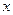 轴有两个交点,由题意,要使这两个
轴有两个交点,由题意,要使这两个交点横坐标
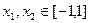 ,当且仅当:
,当且仅当: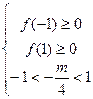 , 解得:
, 解得: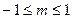

(2)对任意
 都有
都有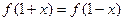 ,所以
,所以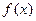 图像关于直线
图像关于直线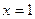 对称,
对称,所以
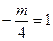 ,得
,得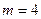 .所以
.所以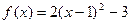 为
为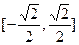 上减函数.
上减函数. 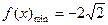 ;
;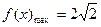 .故
.故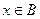 时,
时,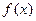 值域为
值域为 .
. (3)令
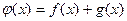 ,则
,则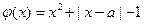
(i)当
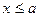 时,
时,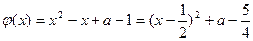 ,
,当
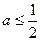 ,则函数
,则函数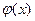 在
在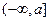 上单调递减,
上单调递减,从而函数
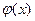 在
在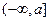 上的最小值为
上的最小值为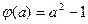 .
.若
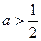 ,则函数
,则函数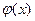 在
在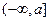 上
上 的最小值为
的最小值为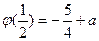 ,且
,且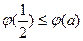 .
.(ii)
 当
当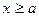 时,函数
时,函数
若
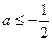 ,则函数
,则函数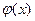 在
在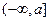 上的最小值为
上的最小值为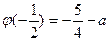 ,且
,且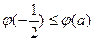
若
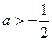 ,则函数
,则函数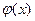 在
在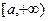 上单调递增,
上单调递增,
从而函数
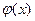 在
在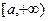 上的最小值为
上的最小值为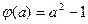 .
.综上,当
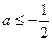 时,函数
时,函数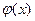 的最小值为
的最小值为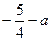
当
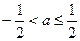 时,函数
时,函数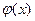 的最小值为
的最小值为
当
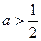 时,函数
时,函数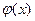 的最小值为
的最小值为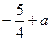
略

练习册系列答案
相关题目
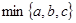 表示
表示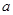 ,
,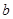 ,
,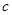 三个数中的最小值.
三个数中的最小值.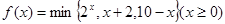 ,则
,则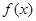 的最大值为 ( )
的最大值为 ( )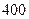 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时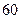 吨的速度向池中注水.已知
吨的速度向池中注水.已知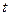 小时内向居民供水总量为
小时内向居民供水总量为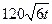 吨
吨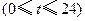 ,问
,问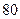 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?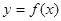 的图象如图①所示,则图②对应函数的解析式可以表示为
的图象如图①所示,则图②对应函数的解析式可以表示为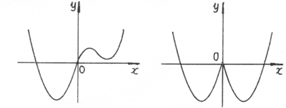
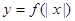
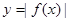
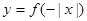
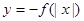
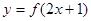 是定义在R上的奇函数,函数
是定义在R上的奇函数,函数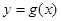 的图象与函数
的图象与函数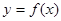 的图象关于直线
的图象关于直线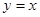 对称,则
对称,则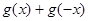 的值为
的值为 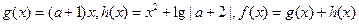 ,其中
,其中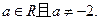
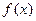 为偶函数,求a的值;
为偶函数,求a的值;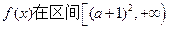 上是增函数,命题q:函数
上是增函数,命题q:函数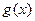 是减函数,如果p或q为真,p且q为假,求a的取值范围。
是减函数,如果p或q为真,p且q为假,求a的取值范围。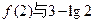 的大小。
的大小。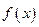 的定义域为
的定义域为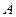 ,若
,若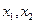
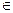
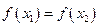
 时总有
时总有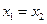 ,则称
,则称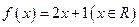 是单一函数,下列命题正确的是____▲____.(写出所有正确答案)
是单一函数,下列命题正确的是____▲____.(写出所有正确答案)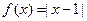
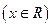 是单一函数;
是单一函数;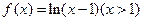 是单一函数;
是单一函数; 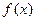 为单一函数,
为单一函数,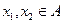 且
且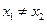 ,则
,则
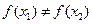 ;
; 定是单调函数.
定是单调函数. 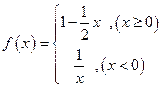 ,若
,若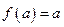 ,则
,则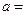
 的零点
的零点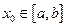 ,且
,且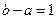 ,
,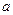 ,
,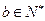 ,则
,则